Quando parliamo di materiali granulari ci riferiamo a sistemi composti da un numero elevato di particelle macroscopiche. Lo zucchero, i cereali, la ghiaia, la sabbia, le polveri, i detriti sono esempi di granulari. Essi sono, dopo l’acqua, le sostanze più comuni con cui l’uomo viene a contatto nella sua vita quotidiana. Una loro caratteristica fondamentale è il fatto che le particelle costituenti, per quanto possano anche essere piccole, sono sempre di dimensioni macroscopiche, dell’ordine cioè delle centinaia di μm, dei mm o più. Questa proprietà ha conseguenze molto importanti sul loro comportamento, spesso non intuitivo, ed è una delle cause principali delle difficoltà che si riscontrano nel costruirne una teoria sistematica e pienamente soddisfacente.
Figura 1: alcuni esempi di materiali granulari che compaiono nella vita di tutti i giorni.
Prima conseguenza è che – per i materiali granulari – la temperatura dell’ambiente è molto poco rilevante. Per un microscopico granello di polline (pochi micron di diametro) abbandonato in un bicchiere di acqua, le fluttuazioni termiche – cioè l’agitazione delle molecole del liquido circostante – hanno un effetto visibile: il polline, come notò Robert Brown nel 1827, fluttua e molto lentamente si sposta da una parte all’altra del bicchiere. Un granello di sabbia (tipicamente più grande e pesante del granello di polline), è quasi completamente insensibile a questa agitazione molecolare. Altra conseguenza è la natura dissipativa delle interazioni: l’energia, a livello macroscopico, non si conserva, da cui l’impossibilità di usare tout court i metodi della meccanica statistica che si usano per i gas e i liquidi molecolari.
Questo a dispetto del fatto che i granulari sono apparentemente molto simili ai gas e ai liquidi. Similmente a un liquido, un granulare può fluire riempiendo una bottiglia ma, a differenza di una generica miscela o soluzione, può risultare assai difficile realizzare un mescolamento omogeneo di due diversi granulari; anzi a volte una miscela di granulari può essere facilmente separato nei suoi grani costituenti (tramite, ad esempio, opportuna vibrazione meccanica). Il problema del mescolamento delle polveri è ben noto in settori di grande interesse applicativo come l’industria farmaceutica.
1. PROPRIETÀ STATICHE
In un recipiente cilindrico di raggio R riempito di un fluido di densità ϱ fino a una quota h, la pressione sul fondo è data dalla legge di Stevino
\([1] P(h)=\rho g h\)
In un recipiente pieno di granulare, la pressione cresce invece con la quota soltanto se h non è molto grande rispetto a R, mentre per grandi valori di h la pressione rimane costante. Questo fenomeno, legge di Janssen, è alla base del funzionamento delle clessidre: Il flusso attraverso il foro è costante a prescindere dalla quantità di sabbia sovrastante. Il meccanismo microscopico responsabile del fenomeno è la formazione di invisibili archi (o, meglio, volte) costituiti da strutture composte da grani che scaricano la pressione sulle pareti laterali. La posizione e il numero di queste strutture sono casuali, svuotando e riempiendo nuovamente il contenitore, le volte si formeranno in numero e posizioni diverse. Questo fenomeno, assente nella maggior parte dei liquidi, può causare forti disomogeneità nella distribuzione di pressione con effetti molto spettacolari sulla stabilità dei silos, che esplodono con relativa facilità (soltanto negli Stati Uniti, si verificano all’incirca 1000 esplosioni l’anno).
Figura 2: esplosioni – certamente inaspettate – di silos.
2. PROPRIETÀ DINAMICHE
In presenza di sollecitazioni esterne – ad esempio una vibrazione continua del contenitore – si può parlare di gas, liquidi, solidi e talvolta persino di vetri granulari a seconda del grado di ordine presente nel fluido. Le differenze tra questi stati di aggregazione della materia – presenti nei fluidi usuali – sono ben note: in un gas si osserva il massimo disordine nelle posizioni e nelle velocità delle molecole (in questo caso i grani); nei liquidi il disordine – per effetto della maggiore densità o minor temperatura – si riduce pur senza arrivare a strutture coerenti e stabili; nei solidi l’ordine è massimo e dà luogo alla capacità di sostenere sforzi esterni; i vetri sono un caso speciale di aggregazione disordinata ma apparentemente stabile, simile ai solidi. Nello studio teorico particolare interesse suscitano gli stati gassosi in cui è possibile ritrovare molte analogie e alcune profonde differenze rispetto ai gas di molecole. Un punto chiave in cui grani e molecole sono diversi è la conservazione dell’energia nelle interazioni: le molecole la conservano sempre, i grani tipicamente la perdono in attriti vari e questo influenza profondamente la teoria, complicandola notevolmente. Ad esempio un gas granulare lasciato a se stesso evolve fino a esaurire tutta la propria energia (un gas di molecole invece rimane in agitazione permanente). Negli esperimenti è necessario fornire energia al gas in modo da ottenere uno stato statisticamente stazionario. L’energia viene tipicamente iniettata agitando il contenitore o una delle sue pareti. Esperimenti di questo tipo – anche molto semplici – mostrano molti fenomeni in cui appaiono inaspettatamente situazioni con qualche tipo di ordine, i cosiddetti “pattern”, che nei fluidi molecolari sono più difficili da ottenere. La teoria di questi stati di ordine “emergente” passa, in molti casi, per la cosiddetta idrodinamica granulare. Questa teoria, in estrema sintesi, cerca di descrivere i fenomeni che avvengono lentamente e “morbidamente”, ignorando il moto preciso dei singoli grani che varia su tempi molto più brevi.
Le equazioni dell’idrodinamica granulare descrivono in modo soddisfacente i fluidi granulari a densità sufficientemente basse e sono importanti per lo studio di molti fenomeni osservati sperimentalmente, come ad esempio fenomeni di convezione, di onde di densità trasversali e, nel caso di miscele di differenti tipi di grani, di fenomeni di segregazione delle varie componenti.
Video dell’esperimento
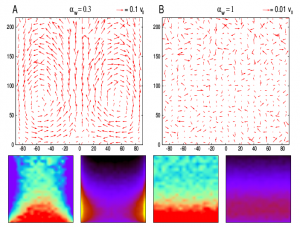
Figura 3: Esempi di ordine granulare: stati stazionari con o senza convezione in un esperimento quasi bidimensionale su un piano inclinato con energia fornita da un pistone vibrante. I grafici a destra – provenienti da simulazioni numeriche – mostrano (in alto) la velocità locale media dei grani, quelli di sotto i campi di energia cinetica media (locale) dei grani e di densità media (locale). Nella parte sinistra dei grafici l’esperimento è riprodotto correttamente, nella parte destra le simulazioni sono state effettuate rimuovendo la dissipazione di energia ai bordi, e questo fa sparire completamente la convezione.
BIBLIOGRAFIA
A. Baldassarri et al.,What is the temperature of a granular medium?, “Journal of physics: condensed matter”, 17, 2005, pp. S2405-S2428.
J. Brey et al., Hydrodynamics for granular flow at low density, “Physical review E”, 58, 1998, pp. 4638-4653.
C. Cercignani, Theory and application of the Boltzmann equation, New York, Elsevier, 1975.
PG De Gennes, Reflections on the mechanics of granular matter, “Physica A”, 261, 1998, pp. 267-293.
J. Duran, Sands, powders, and grains, Berlin, Springer, 2000.
H. Jaeger et al., Granular solids, liquids and gases, “Review of modern physics”, 68, 1996, pp. 1259-1273.
L. P. Kadanoff, Built upon sand: theoretical ideas inspired by granular flows, “Review of modern physics”, 71, 1996, pp. 435-444.
T. Pöschel and S. Luding, eds, Granular gases, Springer, 2001.
A. Puglisi 2014: Transport and Fluctuations in Granular Fluids , Springer, 2014.











