Dispersionless pulse transport in harmonic chains
Ruggero Vaia has published a new article on Physical Review E “Dispersionless pulse transport in mass-spring chains: All possible perfect Newton’s cradles“, R. Vaia, Phys. Rev. E 102, 023005 (2020).
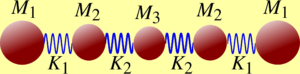
Coherent pulse transmission along an arbitrarily long mass-spring chain is a prototype for several material systems: atom/ion chains, polymer molecules, in 1D, but also 2D and 3D systems with symmetry, such as multilayers.
Nevertheless, this effect cannot be obtained in a chain which is both “harmonic” and “uniform”. That is why theoretical efforts have been mostly devoted to “non-harmonic”, or “nonlinear”, models, where the springs do not obey Hooke’s law. Indeed, such nonlinear models display confined traveling excitations, mostly dubbed solitons. In our recent work published on Phys. Rev. E we show that keeping harmonicity while allowing for “non-uniformity” permits to obtain end-to-end transmission of a pulse over arbitrarily long chains.
We demonstrate that “perfect transmission” can be obtained by suitably modifying the whole mass-spring sequence. For any chain length N there are infinite possible sequences that give perfect pulse transfer: these are classified by the one-to-one correspondence with the sequences of N-1 odd coprime natural numbers. The simplest sequence, i.e. [1, 2, …, N-1] admits an analytic solution.
These achievements could find a wider interest, as the proposed approach constitutes a viable mechanism for efficient energy transfer, e.g., in nanofabricated structures.