Nature Communications : Hyperbolic optics and superlensing from self-induced topological transitions
Claudio Conti and Eugenio Del Re co-authored an interesting work published on Nature Communications demonstrating experimentally self-induced topological transitions from elliptical to hyperbolic k-space manifolds in room-temperature photorefractive KTN.
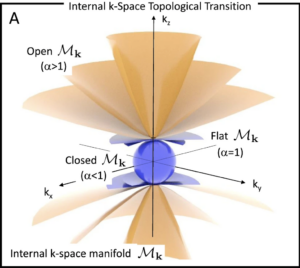
llustration of the internal k-space nonlinear transition as the isofrequency surface passes from an closed-surface topology (α < 1, blue shade) to an open-surface topology (α > 1, yellow shade)
A hyperbolic medium will transfer super-resolved optical waveforms with no distortion, support negative refraction, superlensing, and harbor nontrivial topological photonic phases. Evidence of hyperbolic effects is found in periodic and resonant systems for weakly diffracting beams, in metasurfaces, and even naturally in layered systems. At present, an actual hyperbolic propagation requires the use of metamaterials, a solution that is accompanied by constraints on wavelength, geometry, and considerable losses. We show how nonlinearity can transform a bulk KTN perovskite into a broadband 3D hyperbolic substance for visible light, manifesting negative refraction and superlensing at room-temperature. The phenomenon is a consequence of giant electro-optic response to the electric field generated by the thermal diffusion of photogenerated charges. Results open new scenarios in the exploration of enhanced light-matter interaction and in the design of broadband photonic devices.
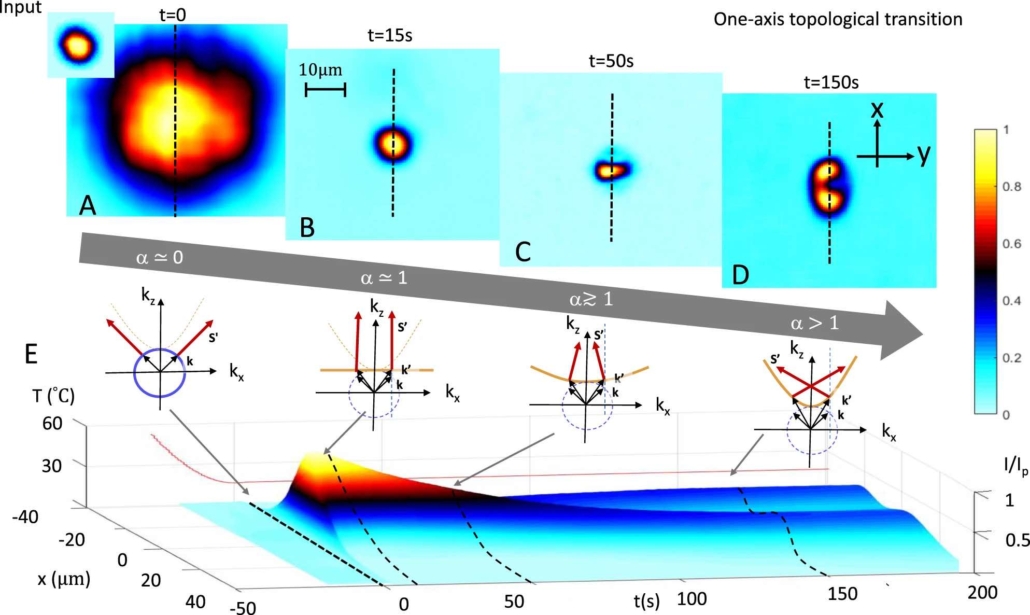
A) Transverse xy intensity distribution I normalized to the peak intensity of the beam Ip at the input facet as transmitted by the mask (inset) that diffracts to the output after Lz = 2.2 mm propagation to 72 μm (FWHM) for t = 0 (i.e., α = 0). B) Output distribution for the scale-free optics regime (t = 15 s and corresponding α = 1). C) The beam now self-induces the transition at t = 50 s, leading to D the signature non-diffracting splitting regime for t > 150 s (α > 1). E The self-induced transition seen in time (and corresponding estimated value of α) using the x intensity profile (dashed lines in A–D)