Long-Lived Higgs Modes in Strongly Correlated Condensates in Physical Review Letters
ISC-Director José Lorenzana has recently collaborated on a compelling research work that appeared in Physical Review Letters. J. Lorenzana and G. Seibold, Long-Lived Higgs Modes in Strongly Correlated Condensates, Phys. Rev. Lett. 132, 026501 (2024).
Condensed matter physics and high-energy physics has cross fertilizing each other for decades. One paradigmatic example is superconductivity, where Anderson’s mechanism giving mass to the Goldstone mode in a superconductor was taken by Higgs to explain mass generation in the
Standard model of elementary particles. Pressed by a referee, Higgs did an additional prediction of a resonance, a new particle now dubbed the Higgs boson which granted him the Nobel Prize in physics in 2013 after the particle was observed at CERN’s Large Hadron Collider.
Naturally, the next question is where is the Higgs boson in the superconductor? Unfortunately, superconductors and Standard model are not identical and the Higgs resonance in the superconductor overlap which a continuum of excitations which make its short-lived and its observation very difficult. Now, Seibold and Lorenzana pointed out that this is true in the ordinary superconductor predicted by the conventional weak coupling (BCS) theory. However, for a strong coupling superconductor, they find that the Higgs mode is long-lived and can be detected. After their work was posted, an experimental group in Hamburg found a long-lived Higgs mode in a condensate of fermionic ultracold atoms precisely in the strong coupling regime predicted by the theory.
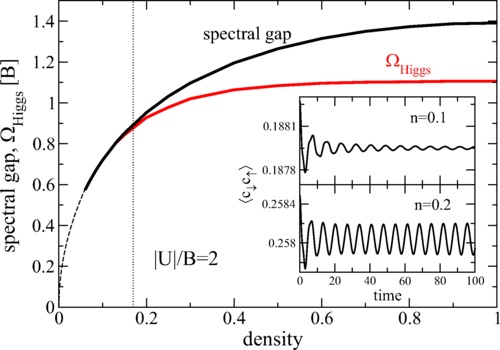
Main panel: Time-dependent Gutzwiller approximation (TDGA) energies of the spectral gap 2Δ (black) and the Higgs mode (red) as a function of density for the attractive Hubbard model (|U|/B=2) with a semielliptic density of states (bandwidth B). To the left of the vertical dotted line, the chemical potential falls below the lower band edge. Insets: time dependence of the anomalous correlations for densities n=0.1 and n=0.2, respectively.