The Hyperspin Machine in Nature Communications
Our colleagues Claudio Conti and Marcello Calvanese-Strinati have recently published a beautiful theoretical work showing how coupled parametric oscillators can simulate multidimensional continuous spin models. Read more on Nature Communications, 13 7248 (2022)
Abstract
From condensed matter to quantum chromodynamics, multidimensional spins are a fundamental paradigm, with a pivotal role in combinatorial optimization and machine learning. Machines formed by coupled parametric oscillators can simulate spin models, but only for Ising or low-dimensional spins. Currently, machines implementing arbitrary dimensions remain a challenge. Here, we introduce and validate a hyperspin machine to simulate multidimensional continuous spin models. We realize high-dimensional spins by pumping groups of parametric oscillators, and show that the hyperspin machine finds to a very good approximation the ground state of complex graphs. The hyperspin machine can interpolate between different dimensions by tuning the coupling topology, a strategy that we call “dimensional annealing”. When interpolating between the XY and the Ising model, the dimensional annealing substantially increases the success probability compared to conventional Ising simulators. Hyperspin machines are a new computational model for combinatorial optimization. They can be realized by off-the-shelf hardware for ultrafast, large-scale applications in classical and quantum computing, condensed-matter physics, and fundamental studies.
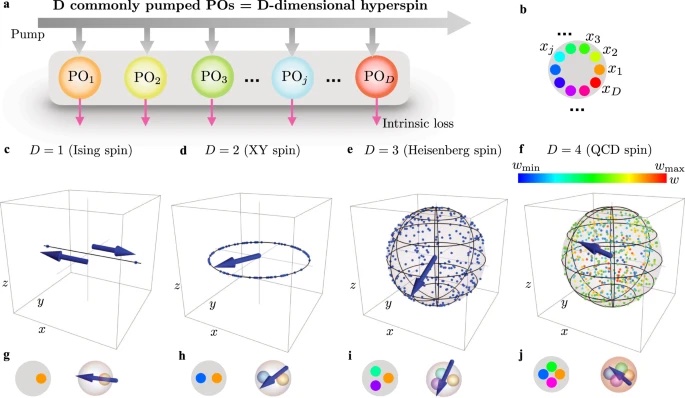
a.The spin consists of D degenerate parametric oscillators (POs) (colored dots) saturating the same pump field (gray arrows and area) with equal intrinsic loss (purple arrows). b Compact representation of the scheme in a. The colored dots denote the D POs, described by dynamical variables x1, …xD, and the gray circle represents the common pump. c, d, e, f Fixed points of the composite PO system. The fixed points lie on the surface of a D-dimensional hypersphere. For D = 1, there are two fixed points on the x-axis representing the two states of an Ising spin; For D = 2, the fixed points lie on a circumference in the xy-plane, encoding the continuous phase of a XY spin; For D = 3, the fixed points lie on the surface of a sphere in the xyz-space, encoding the two angles of an Heisenberg spin; For D = 4, the fixed points are represented by encoding three of the four coordinates into a point within the volume of a sphere in the xyz-space, and the fourth coordinate w is encoded as a color with extremal values wmin and wmax in the colormap. g, h, i, j Left panels are the composite PO representation of the D-dimensional spin as in panel b, while right panels are a three-dimensional representation of the composite PO as a spin σ→ in standard hyperspherical coordinates (blue arrow). For D = 4, borrowing the terminology from QCD, the arrow represents the “vector” xyz-component of the QCD spin, and the color assigned to the outer sphere encodes the “scalar” w-component.