Anomalous Heat Transport in Low Dimensions
Many phenomena in nature occur under nonequilibrium stationary conditions. For instance, an electric current is obtained by applying an electric field along a conductor or heat is transported when a temperature gradient is established between two boundaries of a material. Despite their ubiquiteness and importance in everyday life many aspects of such phenomena are still under debate in the theoretical physics community.
One issue that received a renewed attention concerns the role of spatial constraints. In fact, the response to external forces is intimately related to statistical fluctuations whose importance, in turn, dramatically depends on the system dimensionality. What has thus to be expected when dealing with energy or charge transport in almost one–dimensional system like, say, a nanowire or a DNA molecule?
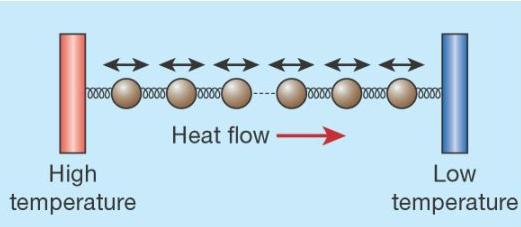
In view of the variety and complexity of specific interactions, simplified microscopic models are an unvaluable tool to provide inferences about transport mechanisms in reduced dimension. A case where this approach revealed unexpected results is the the old problem of heat conduction, already studied by J.J.B. Fourier at the beginning of the XIX century. Indeed, recent simulation studies of toy models of classical low–dimensional fluids and crystals neatly show that the thermal conductivity increases with the system size.
In other words, heat is transported more efficiently the more the system is large (at fixed density and gradient). This amounts to say that the mean free path of the “heat carriers” increases with the length of the sample. Such anomalies disappear only in three dimensions — a scenario very similar to the problem of “long-time tails” in fluids or to localization in disordered media.
Besides the many conceptual problems that motivate the study of energy transport under such strong spatial constraints, there exist a variety of real systems where such anomalies could play a major role. If universality holds, one can reasonably expect that the scaling laws derived for simple models should apply.
The most prominent examples is heat transport in individual single-walled nanotubes (SWNT) that are experimentally demonstrated to display the predicted effects [http://prl.aps.org/abstract/PRL/v101/i7/e075903] as well as the celebrated graphene [http://www.nature.com/nmat/journal/v10/n8/abs/nmat3064.html].
S. Lepri, R. Livi, A. Politi
PhysicsReports
Thermal conduction in classical low-dimensional lattices
Phys. Rep. 377 1 (2003)
M. Buchanan
http://www.nature.com/nphys/journal/v1/n2/full/nphys157.html
Nature Physics
Figure Caption
Simple models versus real materials: modeling anomalous heat conduction in low-dimensional systems of interacting particles (like the nonlinear chain of oscillators in contact with reservoirs at different temperatures T_1 and T_2 shown in the upper part) may be relevant for understanding transport in single-walled carbon nanotubes (depicted in the lower part) and, generally, in other systems where spatial constraints play a crucial role.