Scale-free networks
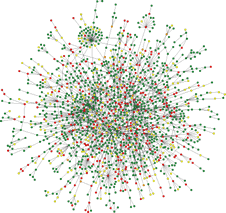
Scale-Free Networks are present in a wide list of phenomena. Examples range from the structure of the Internet and that of the WWW (we shall see in the following that they are different systems) to the interconnections between financial agents or species predation in ecological food webs. Thanks to the simplicity of graph theory it is very easy to provide a network description for different systems. Network components can describe many different real-world units such as Internet providers, electricity providers, economical agents, ecological species, etc. The links between the various components can describe a global behaviour such as the Internet traffic, electricity supply service, market trend, environmental resources depletion, etc. 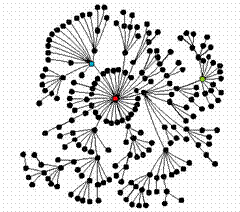 It is clear that the shape of a network and its functionality must be closely related. This means that if we know the topological properties of a food web, this could help to determine the laws governing predations in ecosystems. In principle, we could discover and protect the key species (if any) that form the skeleton of the ecosystem. In a different field, the same theory can help in designing a faster and more efficient Internet network, avoiding possible attacks on its functionality. If it is easy to define a network in almost any field of research, there is no reason why different networks should have a similar behaviour. Yet, from experimental studies, we find that almost all the networks considered here (and many others) share many similar properties (but also maintain many differences). One possible explanation for this universality is that a common formation mechanism acts in different cases. If the nature of this mechanism is understood, this piece of information could be used to predict the future evolution of such objects. More importantly in some cases, not only the global structure (e.g. the cable connection of the Internet) but also the dynamical evolution of the system (e.g. the Internet traffic) are the self-organized result of the interactions between network elements. For the above reasons such systems are a paramount example of the so-called science of `complexity’ whose presence is becoming more and more evident in physics, biology, mathematics, and computer science. Both in scale-free networks and in other complex systems the presence of large-scale correlations is witnessed by the appearance of power law distributions.
It is clear that the shape of a network and its functionality must be closely related. This means that if we know the topological properties of a food web, this could help to determine the laws governing predations in ecosystems. In principle, we could discover and protect the key species (if any) that form the skeleton of the ecosystem. In a different field, the same theory can help in designing a faster and more efficient Internet network, avoiding possible attacks on its functionality. If it is easy to define a network in almost any field of research, there is no reason why different networks should have a similar behaviour. Yet, from experimental studies, we find that almost all the networks considered here (and many others) share many similar properties (but also maintain many differences). One possible explanation for this universality is that a common formation mechanism acts in different cases. If the nature of this mechanism is understood, this piece of information could be used to predict the future evolution of such objects. More importantly in some cases, not only the global structure (e.g. the cable connection of the Internet) but also the dynamical evolution of the system (e.g. the Internet traffic) are the self-organized result of the interactions between network elements. For the above reasons such systems are a paramount example of the so-called science of `complexity’ whose presence is becoming more and more evident in physics, biology, mathematics, and computer science. Both in scale-free networks and in other complex systems the presence of large-scale correlations is witnessed by the appearance of power law distributions.
It seems then natural to spend some part of this book in the description of these particular statistical distributions. Sometimes, as in the case of fractals, these power laws appear in nature and describe geometrical properties (e.g. a wildfire that leaves unburned regions). In other cases, we have natural phenomena whose geometrical properties are regular but whose evolution over time proceeds through power law distributed avalanches (e.g. species extinctions in an ecological system). In scale-free networks (and this is the core of the book) the power laws appear when considering `topological’ quantities such as the degree (defined as the number of edges per vertex). This does not imply that scale-free networks are simply another type of fractals. Rather, the scale-free nature of some real networks might have the same origin as the scale-invariance present in other phenomena. One example could be that of the multiplicative processes that can produce both power laws and log-normal distributions (these can appear as power laws). A similar mechanism can then produce fractals in one case and scale-free networks in another. This common origin explains why in most of the cases scale-free networks present a series of properties usually associated with self-organization and complexity. They effectively start from small collections of vertices and edges and in their growth, they develop some characteristic features as a power law distributed frequency for the degree. It is worth noting that, power law distributions also appear in other quantities like clustering, betweenness, and average degree of the neighbours.
Contacts:
Guido Caldarelli
Publications



