Inertial Particles in Turbulent Flows
We already mentioned that enhanced mixing is probably one of the most distinguishing feature of turbulence. When a turbulent flow is seeded with particulate matter having a finite size and/or density different from that of the carrier fluid, new features appear. The figure on the left show the instantaneous position particles which are heavier (e.g. water drops in air) resp. lighter (e.g. air bubbles in water) than the carrier fluid. As one can see two features can be identified: heavy/light particles distribute in a very inhomogeneous way (even if the flow is incompressible) forming clusters and voids; heavy and light particles spontaneously segregate visiting different regions of the flow. Both these phenomena find their roots in the presence of inertia (due to the density difference between particles and fluid and to their finite size) — hence the name inertial particles— and they are both very important.

Heavy (red) and Light (blue) particles in a slice of the simulation box, obtained from a direct numerical simulation of turbulence. Note that the two particle classes are segregated and organized in complex clusterized structures. (RIGHT) Fractal dimension of particle clusters as a function of both the response time and the density ratio, as estimated from the computation of the Lyapunov dimension. Note that light (B>1) particles tend to clusterize much more than heavy (B<1) ones, and that there is an optimal Stokes number for observing maximal clustering.
For instance, the presence of clusters enhances the probability of two particles to be at interaction distance for e.g. collisions or chemical reactions. Collisions rates are further enhanced by the velocity difference among two particles, which can be rather large thanks to inertia which makes particle velocities uncorrelated with that of the fluid. The one just described seems to be an important mechanism responsible for the formation of rain drops in warm clouds, which is an important still open problem. Understanding the statistical and dynamical properties of inertial particles together with their clustering is relevant also to aerosol physics whose importance in climatic issues, pollution or in human health cannot be understimated.
Typically inertial particles are characterized in terms of two “control paramenter”: the Stokes number (St) measuring the response time of particles in unit of the smallest time scale of the flow, and the mas density ratio with respect to the fluid (B). Therefore, the main issue is to understand the behavior of the dynamics and statistics particles as a function of both St and B.
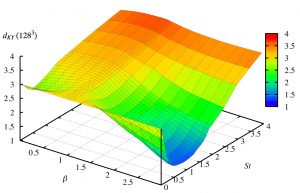
Fractal dimension of particle clusters as a function of both the response time and the density ratio, as estimated from the computation of the Lyapunov dimension. Note that light (B>1) particles tend to clusterize much more than heavy (B<1) ones, and that there is an optimal Stokes number for observing maximal clustering.
Further, properly characterizing the segregation among particles with different inertia (i.e. different density) would help both in devising new mass separation strategies and also in developing new tools for probing specific regions/structures of turbulent flows.
For their importance in enviromental and industrial applications inertial particles are subject of an ongoing research activity since the last five years. Our reasearch focused on several aspects of the problem. Theoretical studies in which the properties of the velocity field are prescribed and well under control allowed us to achieve a better understanding of the mechanisms at the basis of clustering and to develop effective models for the collision rate among particles (click here for details) [1]. In particular, the problem of polydisperse particle suspensions have been approached borrowing tools and ideas from dynamical systems theory –such a strange attractors with multifractal measures–, allowing us to achieve a suitable theoretical language for the description of inertial particles [1].
Still considering stochastic flows mimiking true turbulent ones, but with some simplification expecially concerning time correlations, it was possible to obtain an (even analytical) understanding of many features of clustering expecially in the very large and very small St asymptotics in both differentiable [2] (mimiking turbulence dissipative scales) and rough [3](mimiking turbulence inertial range) stochastic flows. These results have been extended and summarized in a compact review [4]. In parallel with the investigation of simplified random flow it has been carried on an extensive program of large scale direct numerical simulations of moderately high Reynolds number flows transporting millions of particles having different density and response times this allowed us to achieve a rather systematic characterization of particle clustering [9], acceleration [5,6], Lyapunov exponents [8] and segregation [10] as a function of St and B. For instance, the figure on the right depicts the Lyapunov dimension as a function of the density ratio and of St for particles in a DNS with resolution 1283. Some of these results were also subject of successful comparison with independent experimental results.
Relevant Publications
Stochastic model flows
[1] Clustering and collisions of heavy particles in random smooth flows
J. Bec, A. Celani, M. Cencini and S. Musacchio Phys. Fluids 17 073301 (2005)
[2] Heavy particles in incompressible flows: the large Stokes number asymptotics
J. Bec, M. Cencini and R. Hillenbrand Physica D 226, 11 (2007)
[3] Clustering of Heavy particles in random self-similar flows
J. Bec, M. Cencini and R. Hillenbrand Phys. Rev. E (Rapid Comm.) 75, 025301 (2007)
[4] Stochastic suspensions of heavy particles
J. Bec, M. Cencini, R. Hillerbrand and K. Turitsyn Physica D 237 2037 (2008)
Turbulent realistic flows
[5] Acceleration statistics of heavy particles in turbulence
J. Bec, L. Biferale, G. Boffetta, A. Celani, M. Cencini, A. Lanotte, S. Musacchio, and F. Toschi J. Fluid Mech. 550, 349 (2006)
[6] Dynamics and statistics of heavy particles in turbulent flows
M. Cencini, J. Bec, L. Biferale, G. Boffetta, A. Celani, A. Lanotte, S. Musacchio and F. Toschi J.Turb. 7 , 1 (2006)
[7] On the effects of vortex trapping on the velocity statistics of tracers and heavy particle in turbulent flows
J. Bec, L. Biferale, M. Cencini, A. Lanotte and F. Toschi Phys. Fluids (Letter to the Editor) 18 , 081702 (2006)
[8] Lyapunov exponents of heavy particles in turbulence
J. Bec, L. Biferale, G. Boffetta, M. Cencini, S. Musacchio and F. Toschi Phys. Fluids (Letter to the Editor) 18 , 091702 (2006)
[9] Heavy particle concentration in turbulence at dissipative and inertial scales
J. Bec, L. Biferale, M. Cencini, A. Lanotte, S. Musacchio and F. Toschi Phys. Rev. Lett. 98, 084502 (2007)
[10] Quantifying turbulence induced segregation of inertial particles
E. Calzavarini, M. Cencini, D. Lohse and F. Toschi Phys. Rev. Lett. 101, 084504 (2008)


