Lagrangian Turbulence
Recently, part of the research activity on turbulence has focused on temporal properties of turbulent statistics which are much less known than the equivalent spatial properties, and are expected to bring information on some of the mechanisms responsible for intermittency in turbulence, for example lagrangian motion is strongly affected by the presence of vortical motion around vortex filaments (see Figure 1). The idea is to study correlations of the fluid velocity along the path of fluid elements (Lagrangian point of view), this is indeed necessary to eliminate spurious correlations induced by the so-called sweeping (i.e. the advection of velocity fluctuations on a given scale due to fluctuations taking place over larger scales). Several independent studies demonstrated that Lagrangian statistics is highly nontrivial expecially the role of vortex entraping seems to be crucial in determining the short time (below and around the Kolmogorov time) behavior of the velocity correlation function (this is best illustrated contrasting with the behavior of heavy particles, see also below and [1]).
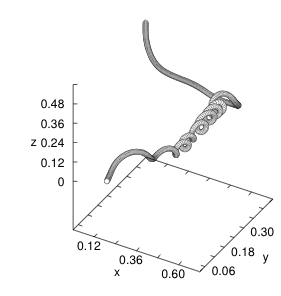
Fig.1 Portion of a particle trajectory demonstrating the presence of events in which the particle is trapped for a long time along a vortex filament of a three-dimensional turbulent flow (figure from L. Biferale, et al Phys. Fluids 17, 021701 (2005).)
We have thus conducted first a detailed comparison between a numerical data set (produced by us) and an experimental one obtained by the group leaded by E. Bodenschatz in Germany (see Ref.[2]) which helped us in recognizing that the quantitative differences between numerical and experimental data were mostly due to statistical biases due to various kind of finite size effects that are unavoidable in experimental studies [2]. Then in collaboration with several experimental and computational groups sparsed in Europe and USA we attempted [3] a detailed comparison among different data sets to determine whether the temporal statistics is universal. As shown in Fig.2 the various data sets obtained in different experimental and numerical flow conditions turned out to be compatible (at least at the level of not too high order statistics, as accessible at present).
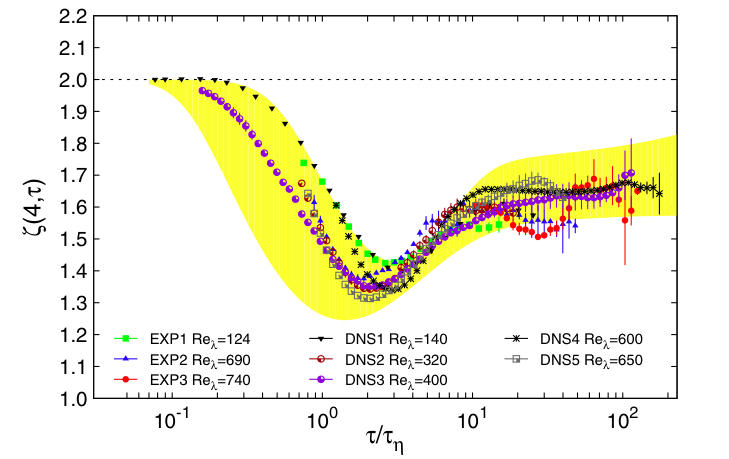
Fig2. The plot on the right show the local slopes (logarithmic derivatives) of the fourth order Lagrangian structure function versus the second order (which is a way to highlight the presence of intermittency, which here means deviation from 2, i.e. the dashed line) obtained from 8 different data sets, see [2] for details. The yellow shaded area represents the prediction of the multifractal model adapted from the Eulerian to the Lagrangian context.
Relevant Publications
[1] On the effects of vortex trapping on the velocity statistics of tracers and heavy particle in turbulent flows
J. Bec, L. Biferale, M. Cencini, A. Lanotte and F. Toschi Phys. Fluids (Letter to the Editor) 18 , 081702 (2006)
[2] Lagrangian Structure Functions in Turbulence: A Quantitative Comparison between Experiment and Direct Numerical Simulation
L. Biferale, E. Bodenschatz, M. Cencini, A.S. Lanotte, N.T. Ouellette, F. Toschi and H. Xu Phys. Fluids 20,065103 (2008)
[3] Universal intermittent properties of particle trajectories in highly turbulent flows
International Collaboration for Turbulence Research A. Arneodo, R. Benzi, J. Berg, L. Biferale, E. Bodenschatz, A. Busse, E. Calzavarini, B. Castaing, M. Cencini, L. Chevillard, R. Fisher, R. Grauer, H. Homann, D. Lamb, A.S. Lanotte, E. Leveque, B. Luethi, J. Mann, N. Mordant, W.-C. Mueller, S. Ott, N.T. Ouellette, J.-F. Pinton, S. B. Pope, S.G. Roux, F. Toschi, H. Xu, P.K. Yeung
Phys. Rev. Lett. 100, 254504 (2008)


