Crisis in Time-Dependent Dynamical Systems on PRL cover
Interesting work by ISC researcher Simona Olmi and ISC associate Antonio Politi on PRL cover.
S. Olmi and A. Politi, Crisis in Time-Dependent Dynamical Systems, Phys. Rev. Lett. 134, 147202 (2025)
Abstract
Many dynamical systems operate in a fluctuating environment. However, even in low-dimensional setups, transitions and bifurcations have not yet been fully understood. In this Letter we focus on crises, a sudden flooding of the phase space due to the crossing of the boundary of the basin of attraction. We find that crises occur also in nonautonomous systems although the underlying mechanism is more complex. We show that in the vicinity of the transition, the escape probability scales as exp[−α (ln δ)2], where δ is the distance from the critical point, while α is a model-dependent parameter. This prediction is tested and verified in a few different systems, including the Kuramoto model with inertia, where the crisis controls the loss of stability of a chimera state.
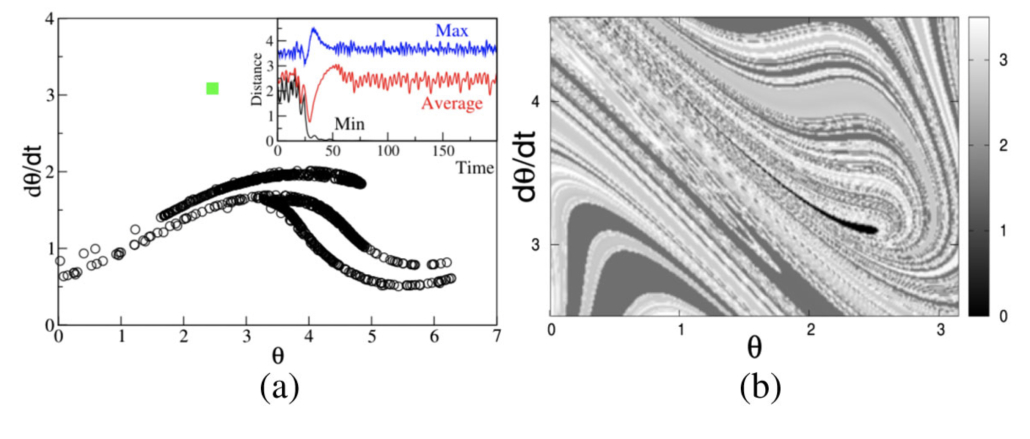
(a) Snapshot of the Kuramoto model in the phase plane. The green square denotes the cluster position, while the open circles denote the dust. Inset: time dependence of the dust-cluster distance in the presence of a migration event. The blue (red) curve identifies the maximal (average) Euclidean distance between the dust and the cluster. The black curve identifies the distance between the cluster and the nearest dust oscillator. Around t=100 the minimal distance virtually vanishes, indicating the occurrence of a migration event. (b) Basin of attraction of the cluster. The grayscale in panel (b) identifies the Euclidean distance of a probe oscillator from the cluster after a time te=100. Initial conditions are varied in a grid of size 0.01 in both directions. The cluster is initially in (2.48160,3.12).


