Thermodynamic Limits of Sperm Swimming Precision – PRX Life
In PRX Life Thermodynamics Reveals Coordinated Motors in Sperm Tails
Thermodynamic Limits of Sperm Swimming Precision, C. Maggi, F. Saglimbeni, V. Carmona Sosa, R. Di Leonardo, B. Nath, and A. Puglisi in PRX Life
Abstract
Sperm swimming is crucial to fertilize the egg, in nature and in assisted reproductive technologies. Modeling the sperm dynamics involves elasticity, hydrodynamics, internal active forces, and out-of-equilibrium noise. Here we give experimental evidence in favor of the relevance of energy dissipation for sperm beating fluctuations. For each motile cell, we reconstruct the time evolution of the two main tail’s spatial modes, which together trace a noisy limit cycle characterized by a maximum level of precision pmax. Our results indicate pmax∼102s−1, remarkably close to the estimated precision of a dynein molecular motor actuating the flagellum, which is bounded by its energy dissipation rate according to the thermodynamic uncertainty relation. Further experiments under oxygen deprivation show that pmax decays with energy consumption, as it occurs for a single molecular motor. Both observations are explained by conjecturing a high level of coordination among the conformational changes of dynein motors. This conjecture is supported by a theoretical model for the beating of an ideal flagellum actuated by a collection of motors, including a motor-motor nearest-neighbor coupling of strength K: When K is small the precision of a large flagellum is much higher than the single motor one. On the contrary, when K is large the two become comparable. Based upon our strong-motor-coupling conjecture, old and new data coming from different kinds of flagella can be collapsed together on a simple master curve.
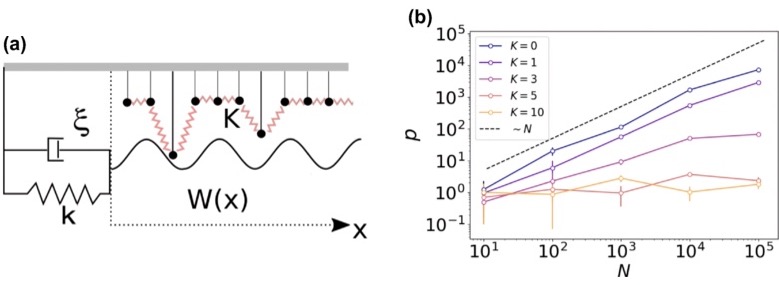
Theoretical model. (a) Sketch of the model. (b) Precision p versus number of motors N for different choices of the coupling parameter K, showing the O(N) scaling for uncoupled motors (K=0) and the O(1) scaling for large K. In all the simulations we have used α=η=0.5, k/ξΩ=10, and αNU0/Ωℓ2ξ=0.6. The error bars are obtained to error propagation based upon the error in the measurement of D. Such error is the estimated standard deviations of D in the nonlinear least-squares fit of the exponential decay of the phase correlation.


