Difetti e sincronizzazione in mezzi oscillatori disomogenei di Massimo Cencini

Massimo Cencini ci parla del problema della sincronizzazione tra oscillatori in presenza di disomogeneità spaziali oggetto di un suo recente lavoro di ricerca. 

 

Sopra: esperimento nell’intestino di gatto. Sotto: simulazioni.

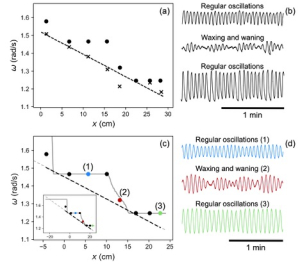
L’accoppiamento tra oscillatori in sistemi estesi spazialmente tende a bloccare loro frequenza su un valore comune. In presenza di non-omogeneità spaziali, il blocco di regioni diverse a frequenze differenti porta alla parcellizzazione, ovvero a una serie di cluster sincronizzati (detti plateau). Motivati dalla dinamica ritmica nei sistemi fisiologici, come l’intestino dei mammiferi o le arteriole celebrali, consideriamo un modello di Ginzburg-Landau (GL) con un gradiente di frequenze naturali. Determiniamo

Le diverse fasi del sistema.

la legge di scala per il numero di plateau e la loro lunghezza tipica in funzione dei parametri dinamici. I plateau sono separati da difetti, nei quali l’ampiezza del campo GL si annulla e le differenze di fase vengono azzerate.

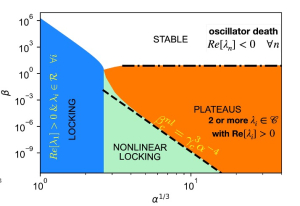
In questo lavoro mettiamo in relazione il diagramma di fase della stabilità e i precursori dei difetti con lo spettro dell’operatore non-hermitiano di Bloch-Torrey, originariamente introdotto per la risonanza magnetica nucleare.

Scaling del numero di plateaus.

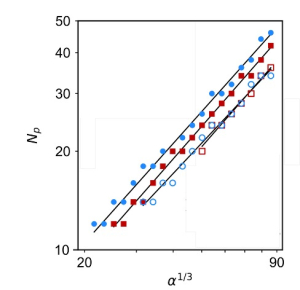
Il sistema è completamente sincronizzato o nel regime dominato dalla teoria lineare, se c’è un solo autovalore positivo, o con un meccanismo non-lineare quando ci sono più coppie di autovalori complessi coniugati. Quest’ultima fase diventa instabile a causa di un meccanismo di diffusività negativa che viene descritto analiticamente nel regime asintotico di forti gradienti. Nel regime di parcellizazione mostriamo la presenza di uno scaling universale del numero di plateaus in funzione dei paramtri adimensionali del sistema.

Bibliografia:

Sellier-Prono, M. Cencini, D. Kleinfeld, & M. Vergassola arxiv:2502.09264 (in review su PRL 2025)