Human Dynamics
Until now, the study of human dynamics has been done only qualitatively. Actually, the present possibility to have quantitative data on the kind and nature of social relationships through social networks is driving a rapid change in the field. Thanks to the emergence of detailed datasets that capture human behavior, we can now follow specific human actions in ultimate detail. One of the first measurable quantity with which one can describe the relationship between humans is the timing and order with which we perform specific tasks. More specifically we want to know if it is possible to model the timing of a series of actions like receiving a phone call, sending an email, booking a flight etc. As in many other complex systems the traditional models have assumed so far that the timing of human actions is random. Some seminal papers by Barabasi and coauthor show that this is not the case. Rather the dynamics of many social, technological and economic phenomena are distributed along a fat tail distribution, that is to say the waiting time for a task to be executed follows a non-Poisson statistics, characterized by bursts of rapidly occurring events separated by long periods of inactivity. More interestingly it is simple to show that the bursty nature of human behaviour is a consequence of a decision-based queuing process: when individuals execute tasks based on some perceived priority, the timing of the tasks will be heavy tailed, with most tasks being rapidly executed, whereas a few experience very long waiting times. In contrast, random or priority blind execution is well approximated by uniform inter-event statistics.
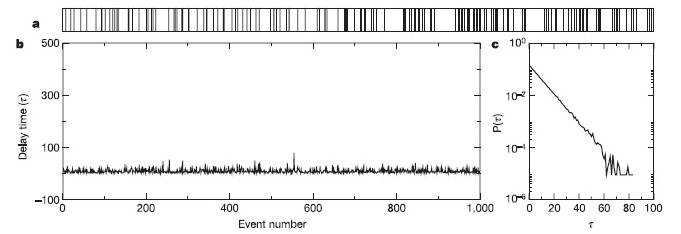
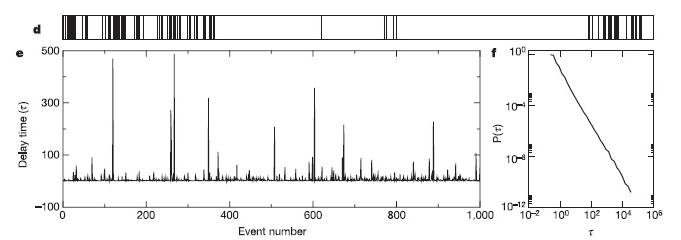
The differences between Poisson and heavy-tailed behaviour are striking: a Poisson distribution (above) decreases exponentially, forcing the consecutive events to follow each other at relatively regular time intervals and forbidding very long waiting times. In contrast, the slowly decaying, heavy-tailed processes (shown below) allow for very long periods of inactivity that separate bursts of intensive activity.
These finding have important implications, ranging from resource management to service allocation, in both communications and retail. We can model the human activity are based on Poisson processes, by assuming that in a dt time interval an individual (agent) engages in a specific action with probability qdt, where q is the overall frequency of the monitored activity. This model predicts that the time interval between two consecutive actions by the same individual, called the waiting or inter-event time, follows an exponential distribution. Since this model does not reproduce the observed data A.-L Barabasi introduced a new model of human dynamics. In this case an individual has a priority list with L tasks, each task being assigned a priority parameter xi, where is chosen from a r(x) distribution and i goes from 1 to L. At each time step the agent selects the highest-priority task from the list and executes it, removing it from the list. At that moment a new task is added to the list, its priority xi being again chosen from r(x). This simple model ignores the possibility that the agent occasionally selects a low-priority item for execution before all higher-priority items are done. This can be incorporated by assuming that the agent executes the highest-priority item with probability p, and with probability (1-p) executes a randomly one. This model in the simplest assumption that the number of tasks is kept fixed can be solved exactly by mapping the problem into a one-dimensional process of Invasion Percolation as shown by A. Gabrielli and Guido Caldarelli. We are currently studying generalization to time dependent priorities and number of tasks.
Further material
Darwin’s letter dataset
A.-L. Barabasi publications
ISC-Sapienza publications