Role of microscopic chaos to macroscopic transport
The discovery that simple deterministic nonlinear systems could display dynamical evolution characterized by a randomness similar to stochastic processes changed very much researchers’ attitude toward determinism and predictability of natural phenomena. Determinstic chaos has been successfully invoked to interpret several irregular behaviors, however its role to the fundaments of statistical physics still remains debated in modern statistical mechanics. In other terms, one is tempted to think that a macroscopic system with chaotic microscopic interactions is more robust with respect to statistical mechanical principles thant the same system with non-chaotic interactions. This particularly controversial issue concerns the role of deterministic chaos for the validity and consistency of statistical approaches.
Our activity rexamines such an issue in the equivalent re-fomulation “Is there any observable signature of microscopic chaos on macroscopic phenomena?” by taking inspiration from the problems of transport in deterministic systems. Transport phenomena are the right context to explore the link between dynamical and statistical properties.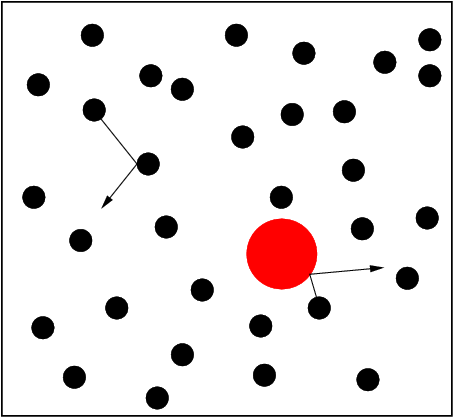
W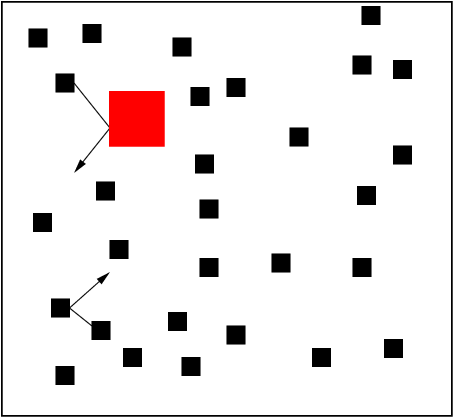
e compared the diffusion properties of a non-chaotic (Figure on the left) system with the same properties of its chaotic counterpart (Figure on the right) to detect the differences in trasport behaviour due to the presence of chaos [1,2].
Figure: (left) Non-chaotic model for diffusion of a mass impurity (in red). Here square particles collide without defocusing, so that chaos is absent. (right) The equivalent chaotic model where disks defocuses their trajectories at each collision may inducing chaos.
Two deterministic models for Brownian motion are investigated by means of numerical simulations and kinetic theory arguments [1]. The first model consists of a heavy hard disk immersed in a rarefied gas of smaller and lighter hard disks acting as a thermal bath. The second is the same except for the shape of the particles, which is now square. The basic difference of these two systems lies in the interaction: hard core elastic collisions make the dynamics of the disks chaotic whereas that of squares is not. Remarkably, this difference is not reflected in the transport properties of the two systems: simulations show that the diffusion coefficients, velocity correlations and response functions of the heavy impurity are in agreement with kinetic theory for both the chaotic and the non-chaotic model. The relaxation to equilibrium, however, is very sensitive to the kind of interaction. These observations are used to reconsider and discuss some issues connected to chaos, statistical mechanics and diffusion.
References
[1] F. Cecconi, M. Cencini and A. Vulpiani “Transport properties in chaotic and non-chaotic many particle systems” J. Stat. Mech., P12001 (2007).
[2] F. Cecconi, M. Cencini, M. Falcioni and A. Vulpiani, “Brownian motion and diffusion: from stochastic processes to deterministic chaos.” Chaos 15, 026102 (2005).
[3] M. Cencini, F. Cecconi, A. Falcioni and A. Vulpiani,
“The role of chaos for the validity of statistical mechanics”, The Fermi-Pasta-Ulam Problem Eds. G. Gallavotti, Lecture Notes in Physics, Vol. 728 p.123 (Springer-Verlag, Berlin, 2007)
