Spatially correlated random walks and turbulence
The wide applicability of the random walks (RW) to natural phenomena relies just on the possibility to introduce appropriate generalizations on the probabilistic nature of displacements. A straightforward generalization is realized by assuming correlations in displacements to obtain the so called correlated random walks (CRW).
This possibility extends also to a set of particles distributed in space leading to the definition of spatially correlated random walks. In this case the issue concerns what particle distribution emerges from reiterated displacements of the particles and how its properties can be directly inferred from the knowledge of the statistical correlation of the displacements.
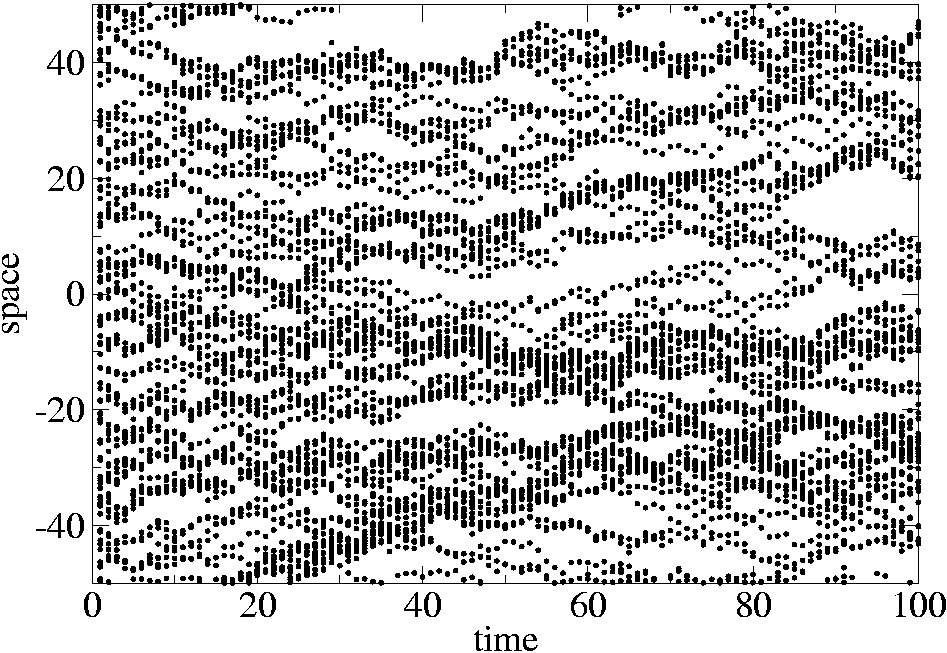 From the exact single step evolution equation [1] of the two-point correlation function of a particle distribution subjected to a stochastic displacement field u(x), we derive different dynamical regimes when u(x) is iterated to build a velocity field. First we show that spatially uncorrelated fields u(x) lead to both standard and anomalous diffusion equation. When the field u(x) is spatially correlated each particle performs a simple free Brownian motion, but the trajectories of different particles result to be mutually correlated [2]. The two-point statistical properties of the field u(x) induce two-point spatial correlations on the particle distribution satisfying a simple but non-trivial diffusion-like equation. These displacement-displacement correlations lead the system to three possible regimes: coalescence, simple clustering and a combination of the two.
From the exact single step evolution equation [1] of the two-point correlation function of a particle distribution subjected to a stochastic displacement field u(x), we derive different dynamical regimes when u(x) is iterated to build a velocity field. First we show that spatially uncorrelated fields u(x) lead to both standard and anomalous diffusion equation. When the field u(x) is spatially correlated each particle performs a simple free Brownian motion, but the trajectories of different particles result to be mutually correlated [2]. The two-point statistical properties of the field u(x) induce two-point spatial correlations on the particle distribution satisfying a simple but non-trivial diffusion-like equation. These displacement-displacement correlations lead the system to three possible regimes: coalescence, simple clustering and a combination of the two.
In this framework we have studied the dynamics of the two-point statistics of the Kraichnan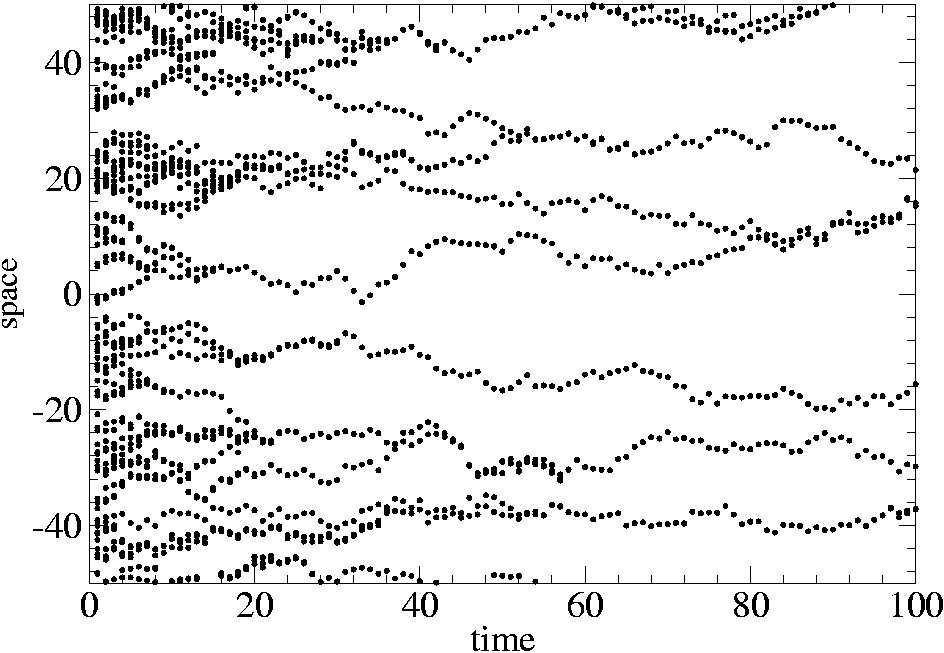 ensemble which describes the transport of a passive pollutant by a stochastic turbulent flow characterized by scale invariant structure functions. The fundamental equation of this problem [3] consists of the Fokker Planck equation for the twopoint correlation function of the density of particles performing spatially correlated Brownian motions with scale invariant correlations.
ensemble which describes the transport of a passive pollutant by a stochastic turbulent flow characterized by scale invariant structure functions. The fundamental equation of this problem [3] consists of the Fokker Planck equation for the twopoint correlation function of the density of particles performing spatially correlated Brownian motions with scale invariant correlations.
This problem is equivalent to the stochastic motion of an effective particle driven by a generic multiplicative noise. The main result is an alternative and more intuitive approach to the problem with respect to previous mathematical formulations [5]. leading to the same conclusions. The general features of this new approach make possible to fit it to other more complex contexts [4].
References
[1] A. Gabrielli, “Point processes and stochastic displacement fields”, Phys. Rev. E., 70, 066131 (2004).
[2] A. Gabrielli, F. Cecconi, “Diffusion, super-diffusion and coalescence from single step” J. Stat. Mech. P10007 (2007).
[3] A. Gabrielli and F. Cecconi, “Clustering and coalescence from multiplicative noise: the Kraichnan ensemble“, J. Phys. A: Math. Gen. 41, 235003 (2008).
[4] F. Cecconi, G. Gonnella and G.P. Saracco, “Kinetics of self-induced aggregation in Brownian particles“, Phys. Rev. E 75, 031111 (2007).
[5] Gawedzki and Vergassola Physica D 138, 63 (2000).


