Granular Gases to explore Non-Equilibrium Statistical Mechanics
How do properties of molecular trajectories reflect on large scale transport and relaxation properties? Is it possible to directly and experimentally verify the Boltzmann’s program, connecting the microscopic level to the macroscopic description? Can we zoom into an out-of-equilibrium fluid and reveal, in the laboratory, its underlying microscopic reversibility? These are some of the questions addressed by the GRANULARCHAOS project, funded by an IDEAS grant (originally selected by ERC and then funded by italian FIRB) for five years.
 The aim of the GRANULAR-CHAOS project is to unravel, through models and experimental examples taken from the physics of granular matter, the rich entanglement of concepts that, even if already assembled in a complete and closed physical theory by Boltzmann more than 100 years ago [1], still stimulates debates, questions and doubts. In the 20th century the theory of dynamical systems has achieved a long series of results in the effort of connecting the microscopic world to the macroscopic one, developing the seminal Boltzmann’s ideas of a deterministic mechanics that can become probabilistic, paving the way to the understanding of how microscopic laws of motion can combine together to give the macroscopic phenomena of transport.
The aim of the GRANULAR-CHAOS project is to unravel, through models and experimental examples taken from the physics of granular matter, the rich entanglement of concepts that, even if already assembled in a complete and closed physical theory by Boltzmann more than 100 years ago [1], still stimulates debates, questions and doubts. In the 20th century the theory of dynamical systems has achieved a long series of results in the effort of connecting the microscopic world to the macroscopic one, developing the seminal Boltzmann’s ideas of a deterministic mechanics that can become probabilistic, paving the way to the understanding of how microscopic laws of motion can combine together to give the macroscopic phenomena of transport.
This topic is recognized to be of capital relevance in the modern program of investigation of the natural world, since it appears, with incontrovertible evidence, that the mere knowledge of rules governing the elementary units of matter is largely insufficient to explain the behavior of most of phenomena surrounding us. Deepening its roots in the work of Boltzmann, Gibbs and Poincare, going through the groundbreaking description of Brownian Motion given by Einstein in 1905, the work of theorists in subjects like mechanics, probability theory, dynamical systems and finally chaos theory, has produced a rich and sophisticated formalism able to describe non-equilibrium systems. In idealized situations, chaos was suggested to be responsible of the way microscopic deterministic laws of motion lead to non-equilibrium phenomena, i.e. transport and entropy production [2]. Other idealized models have demonstrated the lack of universality of this scenario, showing how transport can be observed in non-chaotic systems [3], leading to alternative ideas and characterizations in terms of finite size instabilities and periodic orbit recurrence [4].
At the same time, a growing effort has been devoted to link dynamical properties of systems out of thermodynamic equilibrium, to the energy exchanges with the surroundings (thermostats and applied forces). The ambition is to exploit simple mesoscopic (fluctuating) measurements of energy injected or dissipated, to recover information about the system. This approach is the tentative generalization of some classical results achieved between the 30s and the 50s of the 20th century, which assume linear response laws to relate non-equilibrium averages to equilibrium correlation functions (Fluctuation-Response relations [5]) and in some cases give access to trajectory probabilities in terms of entropy variations (Onsager-Machlup theory [6]). Starting with the Fluctuation Relations (FR), continuing with the Crooks and Jarzynski relations obtained some years later, and finally arriving to the more recent works by Derrida et al. and Bertini et al. on dynamical path probabilities, the last 15 years [7] have produced a whole new theoretical framework which encompass the previous linear response theory and goes beyond, to include far from equilibrium situations.
While the state of the art at the theoretical level is advanced and refined, experimental studies devoted to testing the limits of validity of these ideas and results have not reached the same degree of completeness. Chaos theory in itself has received large experimental attention, but its predictive behavior towards macroscopic (spatially extended) non-equilibrium physics suffers from the dramatic difficulty of studying matter (e.g. fluids) at scales of resolution in space-time differing by several orders of magnitude. The ideal experiment should be the observation of a small sample of a dilute molecular gas with a resolution ranging from the mean free path/time of single molecules motion 10-8m, 10-11sec, up to the characteristic time and length scales of gradients of the hydrodynamics behavior of the sample itself, determined by external conditions and boundaries (e.g. 10-2m, 10^-2sec in a laminar fluid). A recent experiment [8], conceived with the aim of getting near the ideal limit of microscopic resolution of Brownian motion, and all the debate and criticism successively developed, are the vivid demonstration of the urgency of this question. In such experiment the authors could not obtain an unambiguous discrimination between chaos and non-chaos because of the finite size limits of the experiment, both at small scales (their time resolution was 1/60 seconds) and at large ones (order 1 second, much smaller than the time needed by the particle to explore the system and experience the eventual presence of periodic orbits).
Also the large theoretical work devoted to far-from-equilibrium relations concerning mesoscopic fluctuationshas been only partially followed by real experiments: the verification of the FR has been done in the laboratory [9], even if in most of the cases a clear connection with the original theorems is missing, since these theorems refer to entropy productions that are well defined only near equilibrium [10] or in terms of dynamical phase-space observables, inaccessible in experiments. A great success has been achieved in the use of one of these relations (the Jarzynski one) to obtain free energy differences between states of a bio-molecule from non-equilibrium measurements of work [11]. In any case the connection between energy exchanges and the entropy functional characterizing the weights of trajectories a la Onsager-Machlup, has not been verified, because of the difficulty to measure both large and small scales in a spatially extended system.
Recently the statistical mechanics community has been attracted by a physical system displaying a large set of surprising behaviors, being prone to theoretical as well as experimental investigation: the granular gas(GG). A GG is a gas made of sand, i.e. of grains of diameter of the order of 10^-4 or 10^-3 m. Since environmental temperature is irrelevant for the dynamics of such “macroscopic” grains, the dilute (“gaseous”) state is obtained through a suitable external driving, such as the shaking of the container. This external driving can be assimilated, in many models not far from reality, to a standard thermostat. Experiments on GG, which are often inspired to phenomena first observed in applied sciences and in the industry, are common and provide a constant source of intriguing problems for theorists as well as important confirmations for granular kinetic theories [12].

In a GG experiment a fast camera is sufficient to keep track of the trajectories of every single grain and gives detailed information about collisions. A large number of grains (order of thousands) may be collected giving place to observable fluid-like behavior. A GG is therefore a natural candidate to answer the original question: it is in fact an extended system where the range between microscopic and macroscopic scales is shrunk of orders of magnitude with respect to classical fluids. It has features which are similar to those of a molecular gas (at least in a suitable range of external parameters), while its dynamics can easily be analyzed at the level of the single-particle trajectory as well as at the coarse-grained level of irreversible non-equilibrium statistical mechanics.
There is, however, one essential difference with respect to molecular gases: inelasticity. During binary instantaneous collisions a fraction of kinetic energy is lost. This difference, which is at the basis of recent failures in the naive application of FR to GG [13] and the proposal of new experiments [14], poses the necessity to re-formulate a dynamical system formalism for inelastic systems, trying to include (and when possible minimize) the effects of this energy loss [15]: it is crucial, in fact, to recognize that the energy dissipation, unavoidable in granular collisions, is not responsible for macroscopic irreversible behavior, but certainly affects it quantitatively and must be taken into account.
In my recent work [13b], I’ve put in evidence that experimental tentatives [13a] of importing the mathematical concepts of dynamical systems theory in the realm of GG, which are non-conservative at the level of the particle-particle interaction, constitute a dangerous activity, prone to errors and confusion. The goal of the first two years of this project is to setup a theoretical framework, made of models and predictions, able to sustain the design in full details of a set of experiments on driven granular materials, focused on the connection between microscopic and macroscopic levels of description. The team in those first two years will pave the way to the experiments, elaborating the formalism and all the theoretical ideas necessary to their realization and constructing a theory which should contain a translation of known ideas from chaos and non-equilibrium statistical mechanics into a language suitable for granular gas investigation.
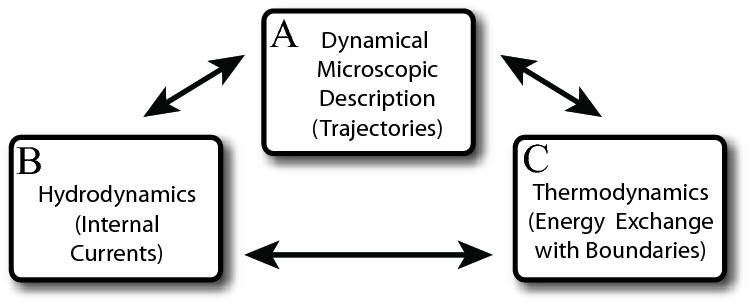
This diagram resumes the scenario that will be used as a reference frame for the whole project. It explains the three main ways of describing and characterizing a spatially extended system driven in a stationary state by balancing external forces and thermostats, such as a driven GG. The exciting fact, with a GG, is that all three characterizations can be obtained in the same experiment, allowing for the first time a direct connection between these different aspects.
A) Dynamical microscopic description: in this context, phase-space trajectories play a crucial role; “static” quantities, such as velocity distributions or spatial (grain-grain) correlations have been experimentally studied in the last few years [16]; two-times quantities have received less attention, and very few studies have been devoted to fluctuation-dissipation relations, while the theory is quite advanced [17]; theory on the other side misses the acquisition of tools from dynamical systems theory, with the noticeable exceptions in [18]; no extensions of the elastic hard-spheres calculations of Kolmogorov-Sinai entropy or the maximum Lyapunov exponents to inelastic gases has been provided to our knowledge, while the question about the chaoticity of a granular gas has in our opinion a non-trivial answer and could enlighten the role of chaoticity and other finite-time instabilities in the relaxation and transport phenomena present in GG; direct measures of coarse-grained phase-space resulting in symbolic dynamics time series are at hand, with the possibility of approximating the transition rates in phase-space and the calculation of Gibbs entropy production, to be compared to calculations of Kolmogorov-Sinai entropy, a connection that is still matter of debate [19]; finally a series of interesting theoretical results [17,20] concern the dynamics of a tracer particle, which is a main link towards point B, being the microscopic seed of macroscopic diffusion; experimental verification of such results is needed, including perturbation-response measurements addressing the validity of fluctuation-dissipation relations.
B) Hydrodynamics: a quite evolved series of studies on granular kinetic theory [21] has made clear that, with certain assumptions, granular hydrodynamics well reproduces numerical experiments, while the limits of such an approach have been clearly delineated [22]; a clear connection with real experiments, on the other side, is still lacking and deserves new studies in the laboratory; a point that is not completely clear, even in the theory, is the zero-current limit [15], which should play the role of reference frame around which currents are linearized to yield linear transport coefficients: how can the linear current-gradient constitutive relation be translated in a linear perturbation-response “experiment”? in granular gas hydrodynamics, in fact, switching on inelasticity without generating currents is not possible; this point has been indirectly addressed by Bonetto et al. [14], when proposing a verification in GG of the FR for the heat exchange: their proposal rely upon a form of the entropy production that is valid in a (limit) regime where the heat flux is constant across a spatially extended region of the system, but it is not clear if such a regime exists for granular hydrodynamics; theoretical and experimental studies on internal current fluctuations are both still missing, while macroscopic kinetic energy fluctuations have been analyzed in [23]; the measure of current fluctuations and two-times correlations would give a direct verification of Green-Kubo formula which have particular forms for a GG [17]; at the level of foundations of hydrodynamic, an open problem is the existence of a scale separation, in time and space, between fast modes and slow modes, whose uncertainty is due to the lack of energy conservation.
C) Thermodynamics: if gravitational potential energy is neglected (otherwise it can be easily taken into account), the total kinetic energy of the gas changes because of two terms, the energy dissipated during collisions $W_{dis}$ and the energy injected-absorbed by the external driving mechanism (here denoted, for the sake of simplicity, with the term thermostat) $W_{inj}$; few numerical studies have addressed the problem of measuring $W_{dis}$, $W_{inj}$, their long-time averages and their finite-time fluctuations, and no experimental studies to our knowledge have tempted such task, with the exception of the Menon and Feitosa [13] experiment which focused on a sub-system and its boundaries with the rest of the gas, obtaining accurate measurements of energy flux fluctuations, but then focusing on a unjustified interpretation in terms of entropy production; the group of Gallavotti [14] proposed an alternative GG experiment closer to the idealized situation of an elastic rarefied gas traversed by a heat flux, in order to verify the Fluctuation Relation; no experimental studies exist on the dependence of energy exchanges (even for averages values) on the external parameters, or dynamical averages during parameter variation (this is in connection with the Hatano-Sasa identity, which has found experimental verification in [11c]); because of the several instabilities (in the density and velocity field), such as the thermal convection instability, the lack of a parameter-dependent study of energy exchange is even more awaited. A re-formulation of thermodynamics for GG, based on macroscopic empirical axioms (i.e. not on statistical mechanics [24]) is an interesting spinoff of this research.
A->B) an elegant connection between transport coefficients, Kolmogorov-Sinai entropy HKS of the invariant fractal set (the so-called repeller) and the sum of its positive Lyapunov exponents has been proposed in [25]; the main critique to such relations comes from the fact that diffusion is observed in non-chaotic system, for which $H_{KS}=0$ [3]; apparently both diffusion properties and estimates from finite length time series analysis (such as the Grassberger and Procaccia method), of the Kolmogorov-Sinai entropy are not able to distinguish between chaotic and non-chaotic systems; in principle they could serve the purpose, but only with a time resolution finer than the mean free time and after a total time larger than the time needed for the particle to explore the whole system and realize its non-chaoticity (i.e. its periodicity or the non exponential instability of periodic invariant set, for open systems).
A->C) a large part of theoretical literature on non-equilibrium physics of last years has focused on this connection; the Gallavotti-Cohen and Evans-Searles fluctuation relations (and the strictly related Crooks and Jarzynski relations) require an identification of an abstract entropy production, defined in term of phase-space contraction rate, with externally measurable energy (heat and work) exchanges: this identification is well supported in simple models, but is much less clear in extended physical systems, such as in GG or in turbulence, where it is most required; an even more ambitious and direct link between phase-space trajectories, microscopic transition rates, and entropies are given by the Bertini et al. and Derrida et al. theories [7], which have not received experimental verification.
B->C) while energy, in a steady state, is on average stationary, putting a trivial constraint on average exchanges between the system and its boundaries, a less trivial (for the quantities involved) balance concerns entropy: it is produced inside the out of equilibrium steady state (in order to keep constant the currents) and it flows through the boundaries with the external thermostats and/or inelastic collisions; as a matter of fact such entropy is only an abstract concept, which becomes well defined only for systems near equilibrium (where linear constitutive relations hold); in a granular gas it becomes even more delicate, since 1) the “sink” extracting energy through inelastic collisions cannot be idealized as a thermostat, i.e. it has not a temperature (better, its temperature is that of the molecular internal degrees of freedom, which is exceedingly smaller than the kinetic temperature defined using the grains as molecules, suggesting that the entropy flow in inelastic collisions is divergingly dominant against all other contributions!); 2) an expansion around the zero-current state seems to us not operatively defined (see above, point B), making unclear how to directly apply linear transport formalism, i.e. in which limit one can write the entropy production as product of currents and generalized forces (gradients); this point is intimately related to the study of fluctuation-dissipation relations: in a granular gas driven from the boundary, internal currents are not developed only by imposing, from the boundaries, a gradient, but it is sufficient to switch on inelasticity.
[1] J. L. Lebowitz, Physics Today, September 1993, page 32
[2] J. R. Dorfman, An introduction to Chaos in Nonequilibrium Statistical Mechanics, Cambridge, 1999; P. Gaspard, Chaos, Scattering and Statistical Mechanics, Cambridge, 1998
[3] C. Dettmann et al., Nature 401, 875 (1999); P. Grassberger and T. Schreiber, Nature 401, 875 (1999); F. Cecconi et al., Physica D 180, 129 (2003)
[4] C. P. Dettmann and E. G. D. Cohen, J. Stat. Phys. 101, 775 (2000)
[5] R. Kubo, Rep. Prog. Phys 28, 255 (1966)
[6] L. Onsager and S. Machlup, Phys. Rev. 91, 1505 and 1512 (1953)
[7] D. J. Evans and D. J. Searles, Phys. Rev. E 50, 1645 (1994); G. Gallavotti and E. G. D. Cohen, Phys. Rev. Lett. 74, 2694 (1995); C. Jarzynski, Phys. Rev. Lett. 78, 2690 (1997); G\ . E. Crooks, Phys. Rev. E 60, 2721 (1999); Bertini et al., Phys. Rev. Lett. 87, 040601 (2001) and Phys. Rev. Lett. 94, 030601 (2005); T. Bodineau and B. Derrida, Phys. Rev. Lett. 92, 180601 (2004\ )
[8] P. Gaspard et al., Nature 394, 865 (1998)
[9] S. Ciliberto and C. Laroche, J. Phys. IV 8, 215 (1998); D. M. Carberry et al., Phys. Rev. Lett. 92, 140601 (2004); N. Garnier and S. Ciliberto, Phys. Rev. E 71, 060101 (2005);\ X. D. Shang et al, Phys. Rev. E 72, 015301 (2005); F. Douarche et al, Phys. Rev. Lett. 97, 140603 (2006); T. Tietz et al, Phys. Rev. Lett. 97, 050602 (2006); V. Blickle et al., Phys. Rev. Lett. 9\ 6 070603 (2006)
[10] S. R. de Groot and P. Mazur, {\em Non-Equilibrium Thermodynamics}, Dover Publications, 1984
[11] G. Hummer and A. Szabo, Proc. Natl. Acad. Sci. U.S.A. 98, 3658 (2001); J Liphardt et al., Science 296, 1832 (2002); F. Ritort, Poincar\’e Seminar 2, 195 (2003); E. H. Trepagnier et al., Proc. Nat. Acad. Sci. 101, 15038 (2004)
[12] T.~P\”{o}schel and S.~Luding (eds.), {\emph{Granular Gases}}, Lecture Notes in Physics, Vol. 564, Springer, Berlin (2001)
[13] K. Feitosa and N. Menon, Phys. Rev. Lett. 74, 164301 (2004); A. Puglisi et al., Phys. Rev. Lett. 95, 110202 (2005)
[14] F. Bonetto et al, J. Stat. Mech. (2006) P05009
[15] S. Aumaitre et al., Eur. Phys. J. B 51, 263 (2006)
[16] W. Losert et al., Chaos 9, 662 (1999); J.S. Olafsen, J.S. Urbach, Phys. Rev. E 60, R2468 (1999); F. Rouyer and N. Menon, Phys. Rev. Lett. 85, 3676 (2000);
[17] J.W. Dufty and J.J. Brey, J. Stat. Phys. 109, 433 (2002); A. Puglisi et al., Phys. Rev. E 66, 061305 (2002); A. Barrat et al., Physica A 334, 513 (2004); A. Puglisi et al., J. Stat. Mech. (2007) P08016
[18] S. McNamara and M. Mareschal, Phys. Rev. E 63, 061306 (2001); A. Fingerle et al., Phys. Rev. Lett. 95, 198001 (2005)
[19] M. Falcioni et al., Phys. Rev. E 71, 016118 (2005)
[20] A. Puglisi et al., Phys. Rev. E. 73, 021301 (2006)
[21] J. Brey et al., Phys. Rev. E 58, 4638 (1998)
[22] I. Goldhirsch, Chaos 9, 659 (1999); L. P. Kadanoff, Rev. Mod. Phys. 71, 435 (1999); A. Puglisi et al., J. Phys.: Condens. Matter 17, S2715 (2005)
[23] Brey et al., Phys. Rev. E 70, 011302 (2004); P. Visco et al., Eur. Phys. J. B. 51, 377 (2006); G. Costantini et al.,J. Stat. Mech. (2007) P08031
[24] E. H. Lieb and J. Yngvason, Phys. Rep. 310, 1 (1999)
[25] P. Gaspard and G. Nicolis, Phys. Rev. Lett. 65, 1693 (1990)

