Inhomogeneities in Cuprates
If the mechanism of high-Tc superconductivity is electronic, to understand the electronic excitation spectrum is as important as to understand phonons was important to develop BCS theory. In this regard charge and spin inhomogeneous states, often found in strongly correlated systems, are interesting because they can support new collective modes, “electronic phonons”, that would not be present in a weakly interacting fluid.
This is analogous to the new vibrational modes that appear when a fluid crystallizes. In particular stripe patterns of charges, which have been observed in cuprates, have oscillatory modes that can couple with carriers and eventually lead to pairing and superconductivity or anomalous Fermi liquid properties. In the last years we have developed a method to compute collective excitations of inhomogeneous strongly correlated systems based on a time-dependent Gutzwiller approximation (GA), named GA+RPA[2, 3, 4, 5, 6]. Our computations reproduce the pattern of magnetic vibrational modes of inhomogeneous high temperature superconductors (HTSC), a key issue that may reveal the mechanism that make them work.
Many theoretical descriptions of cuprates are suited for only one experiment and use “effective” parameters. In our approach one can reproduce a variety of experimental features of La2–xSrxCuO4 in the charge and magnetic channel starting from bare realistic parameters. Results in the one-band Hubbard model (1BHM) and the three-band Hubbard model (3BHM) are quite similar.
1 Ground state properties
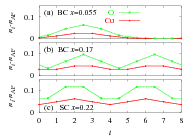
Fig 1. Hole charge minus undoped charge in the 3BHM as a function of atomic position in the direction perpendicular to the stripes for various doping x, symmetry (BC or SC) and charge periodicity d = 9 (a); and d = 4 (b) and (c).
Static properties where computed within the Gutzwiller approximation. Probes which are sensitive to the Cu and O atomic character need to be addressed with the 3BHM. In Fig. 1 we show the evolution of the charge profile with doping in the 3BHM for metallic stripes parallel to the CuO bond. The charge profile in real space has a width of about 4 lattice sites[8]. The width of the stripes defines two regimes: for low doping (a), the stripes do not overlap and therefore are weakly interacting, for high doping (b),(c) stripes overlap.
Recently Abbamonte and collaborators have shown that our charge profile predicted in the 3BHM[8] is in excellent agreement with the profile measured with resonant soft X-ray scattering[9].
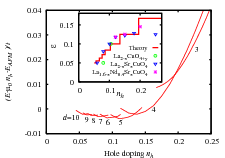
Fig 2. Energy per site as a function of doping for stripes in the 1BHM. The curves are labeled by the charge periodicity d. The inset reports the incommensurability as obtained from the present calculation (line) compared with experiment [11].
In Fig. 2 we show the energy for metallic stripes as a function of doping for the 1BHM. Similar results are obtain with the 3BHM. In each curve the charge periodicity perpendicular to the stripe is fixed and takes integer values (from left to right) d = 10 – 3. In this computations stripes are bond-centered (BC). The energy for site-centered (SC) stripes is slightly lower at small doping but the differences decreases with the system size. At optimum doping both structures become degenerate.
In the inset we plot the incommensurability vs. doping taking into account the range of stability of each solution and compared with experiments from Refs. [11]. The result is a Devil’s staircase. Up to x < 1/8 the plateaux are short and correspond to a number of added holes per unit length along the stripe close to nu= 0.5. As doping increases one jumps from one solution to the other and the density of stripes increases with doping. This explains the behavior of the incommensurability = 1/(2d) = x/(2 nu) = x as seen in neutron scattering experiments in this doping range. For x > 1/8 the right branch of the d = 4 solution is more stable than the nu=0.5 and d = 3 solution due to the overlap effect and one gets a wider plateau explaining the saturation of the incommensurability seen in the experiment.
One can see from the plot of the energy in Fig. 2 that the electron chemical potential mu = –dE/dx is approximately constant in the low doping regime (weakly interacting stripes) whereas it decreases in the overlapping stripe regime. The same behavior was found in a dynamical mean-field study of the one-band Hubbard model[14]. This is in qualitative agreement with experiment[15].
2 Magnetic excitations
The collective excitations in the stripe phase have been reported in Ref. [5]. For bond- and site-centered stripes the excitation spectra are similar, consisting of a low-energy incommensurate acoustic branch which merges into a “resonance peak” at the antiferromagnetic wave vector and several high-energy optical branches. The acoustic branch is similar to the result of theories assuming localized spins whereas the optical branches are significantly different.
Our results are in good agreement with experiments in La1.875Ba0.125CuO4 providing a straightforward explanation of the energy and momentum dependent evolution of the dynamical structure factor in terms of stripes and hence confirming stripes as a robust feature of this system with a firm theoretical basis.
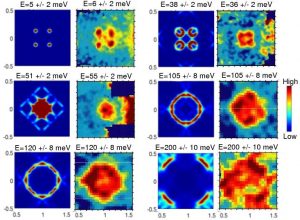
Fig 3. Constant frequency scans of S?(?,q) for BC stripes convolved with a Gaussian (FWHM=0.06 r.l.u.). Panels are shown in pairs with the left panel being our computation and the right panel the experiment from Ref. [17]
3 Optical conductivity
The optical conductivity is qualitatively similar in the three-band and 1BHM. In Fig. 4 we show the result in the 3BHM.
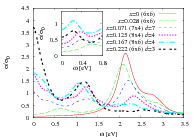
Fig 4. Optical conductivity labeled by doping, system size and, in the case of stripes, interstripe distance. The units of conductivity are given by ?0 = 3.6×102(?cm)-1 with a background dielectric constant ?b = 2.6 The curve labeled x = 0.028 corresponds to the single-hole solution. For larger dopings the figure is an average over the electric field directions parallel and perpendicular to the BC stripes. The inset shows the MIR band excluding the Drude component. We used a Lorentzian broadening of 0.2eV.
Doping induces a doping dependent mid-infrared (MIR) band and Drude weight at zero energy since our stripes are metallic. The MIR band is due to collective lateral fluctuations of the stripe. These lateral fluctuations form a band of excitations as for a violin string and the MIR band corresponds to the zero momentum component.
The “string” fluctuation band is massive due to pinning of the commensurate stripes to the underlaying lattice. However, both the experiment[18] and our computations[3] show that the mass decreases with doping. This is rooted in the quasi-degeneracy found among BC and SC stripes and indicates that stripes form a floating phase at optimum doping. The MIR band produces an absorption at low energy which explains the failure of the Drude model at optimum doping. This suggest that anomalous Fermi liquid properties are rooted in the low energy excitations of the floating phase.
4 Discussion and Conclusions
In cuprates true magnetic long-range order is sometimes detected in experiment[11] however, more often, Bragg peaks are not found. Two possibilities arise: the system may be close to a quantum critical point in the disordered phase (dynamic stripes) or the system may be in the ordered side of the transition but long-range order is not observed because of disorder (glassy stripes). Dynamic stripes have quasi long-range order in time and space whereas glassy stripes at low temperatures have practically long-range order in time but short range order in space as in a structural glass. This latter situation is clear for example in the magnetic channel at low doping, in muon spin-relaxation experiments where below a certain temperature the system develops a static (on the muon time scale) magnetic field which is not necessarily accompanied by Bragg peaks[19], thus the spin rotational symmetry is broken without long range order.
In our calculations we assume long range order both in time and space so why our results resemble experiment? The answer is that at short or intermediate times or length scales the systems appears ordered. Thus in these quantum or classically disordered cases it is not surprising that our results reproduce the experiment as long as the energy scale is not too low (typically tenths of meV in energy) and the length scale not too large (typically of the order of 10 lattice sites).
To conclude we have shown that the GA+RPA approximation allows for a unified description of collective modes in the charge and magnetic channel of striped cuprates. Results are similar in the one-band and the 3BHM although some details may differ in which case the 3BHM is expected to be more accurate. These modes are likely to play an important role in the anomalous properties of cuprates.
References
[1] S. Wakimoto et al. , Phys. Rev. B 60 (1999) 769; Phys. Rev. Lett. 92 (2004) 217004.
[2] G. Seibold, J. Lorenzana, Phys. Rev. Lett. 86 (2001) 2605; G. Seibold, F. Becca, J. Lorenzana, Phys. Rev. B 67 (2003) 085108; G. Seibold, F. Becca, P. Rubin, J. Lorenzana, Phys. Rev. B 69 (2004) 155113.
[3] J. Lorenzana, G. Seibold, Phys. Rev. Lett. 90 (2003) 066404.
[4] J. Lorenzana, G. Seibold, R. Coldea, Phys. Rev. B 72 (2005) 224511.
[5] G. Seibold, J. Lorenzana, Phys. Rev. Lett. 94 (2005) 107006.
[6] G. Seibold, J. Lorenzana, Phys. Rev. B 73 (14) (2006) 144515.
[7] A. K. McMahan, J. F. Annett, R. M. Martin, Phys. Rev. B 42 (1990) 6268.
[8] J. Lorenzana, G. Seibold, Phys. Rev. Lett. 89 (2002) 136401.
[9] P. Abbamonte et al., Nature Phys. 1 (2005) 155.
[10] G. Seibold, J. Lorenzana, Phys. Rev. B 69 (2004) 134513.
[11] J. M. Tranquada et al., Nature (London) 375 (1995) 561; Phys. Rev. Lett. 78 (1997) 338; K. Yamada et al., Phys. Rev. B 57 (1998) 6165.
[12] G. Seibold J. Lorenzana and M. Grilli, cond-mat/0606010.
[13] J. Lorenzana, C. Castellani, C. Di Castro, Europhys. Lett. 57 (2002) 704.
[14] M. Fleck et al., Phys. Rev. Lett. 84 (2000) 4962.
[15] A. Ino et al., Phys. Rev. Lett. 79 (1997) 2101.
[16] R. Coldea et al., Phys. Rev. Lett. 86 (2001) 5377.
[17] J. M. Tranquada et al., Nature (London) 429 (2004) 534.
[18] S. Uchida et al., Phys. Rev. B 43 (1991) 7942.
[19] A. Keren, A. Kanigel, Phys. Rev. B 68 (1) (2003) 012507.
