Synchronization of extended systems
Synchronization is a long known phenomenon dating back to Huygens experiments who observed that suspending two pendula “…in the same wooden beam, the motions of each pendulum in opposite swings were so much in agreement that they never receded the least bit from each other and the sound of each was always heard simultaneously“. In spite of the early discovery, the phenomenon was fully understood much later with the experiments and theoretical analysis of E. V. Appleton and B. Van der Pol in the 20s of last century. Nowadays we know that suitable coupled nonlinear systems can synchronize and that the synchronization can be realized also in chaotic systems.
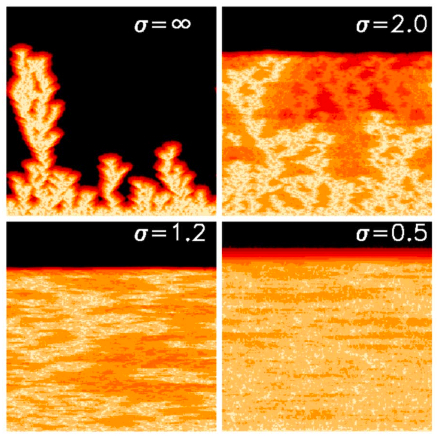
Figure: Synchronization of spatio-temporal chaotic systems when the prevailing instability mechanism is of nonlinear type. [LEFT] Space (horizontal axis) and time (vertical axis) evolution of the synchronization error (i.e. the difference between two coupled replicas of the system) as a function of the range of the interaction close to the synchronization transition. Note that for short range we recover the usual picture of Directed Percolation (DP). [RIGHT] Quantitative comparison of the synchronization transition with DP and Anomalous DP, in particular here we show the critical exponents compared with those known in the literature (black lines). For details see Ref.[2,3].
Remarkably chaotic synchronization can occur also in high dimensional chaotic systems, and in particular in systems with a spatial extension, i.e. systems displaying chaotic spatiotemporal unpredictable evolutions. The presence of many degrees of freedom and, in particular, the spatial extension of these systems convert the bifurcation transition toward the synchronized regime into a non-equilibrium phase-transition, very similar to, e.g., directed percolation or to a variant of the type of transitions (see left panel of the figure) encountered in the Kardar-Parisi-Zhang equation. In particular, after the first observation of Baroni et al (2001) and then Pikovsky & Ahlers(2002), (see also Munoz & Pastor-Satorras (2003)) it has been realized that depending on the type of nonlinearity in the system, more precisely on the prevalence of linear or nonlinear instabilities (see e.g. Cencini & Torcini (2001)), one can observe two universality classes in the synchronization transition of spatially extended chaotic systems: the Directed Percolation or the Multiplicative Noise (which is essentially related to the KPZ equation with boundaries). In a series of works we extended such analogy to the case of spatially chaotic systems with long range interactions [1-3]. In particular, we first analysed the influence of nonlinear mechanisms for the establishment of self-synchronization of all the elements of a system [1], which manifests with the onset of supertransients (exponentially long in the size of the system) that drive the asymptotic behavior in the thermodynamic limit. Then we considered two replicas where it was possible to establish a tight link with the so-called anomalous directed percolation (see Hinrichsen (2007)), where a continuous family of universality classes emerge as a function of the range of the interaction [2] (see Figure).
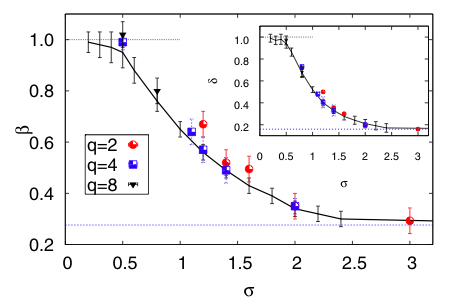
Finally, we completed our program examining generic systems with long range interactions and with linear and nonlinear instabilities at play [3], in this case we identified new phenomena whose theoretical understanding is still lacking. We also studied the case of one and two dimensional systems iwith short range interactions [4], including also the possibility of errors between replicas of the system to approach, on the theoretical side, situations closer to possible experimental realizations of synchronization in spatio-temporal chaotic systems.We have shown that the presence of mismatch is akin to the effect of an external field, see [4].
Relevant Publications
[1] Nonlinearly driven transverse synchronization in coupled chaotic systems
M. Cencini and A. Torcini Physica D 208 , 191 (2005)
[2] Synchronization of extended chaotic systems with long-range interactions: an analogy to Levy-flight spreading of epidemics
C.J. Tessone, M. Cencini and A. Torcini Phys. Rev. Lett. 97 , 224101 (2006)
[3] Chaotic synchronizations of spatially extended systems as non-equilibrium phase transitions
M. Cencini, C.J. Tessone and A. Torcini Chaos 18, 037125 (2008)
[4] Synchronization of spatio-temporal chaos as an absorbing phase transition: a study in 2+1 dimensions
F. Ginelli, M. Cencini, and A. Torcini JSTAT P12018 (2009)


