Theoretical research
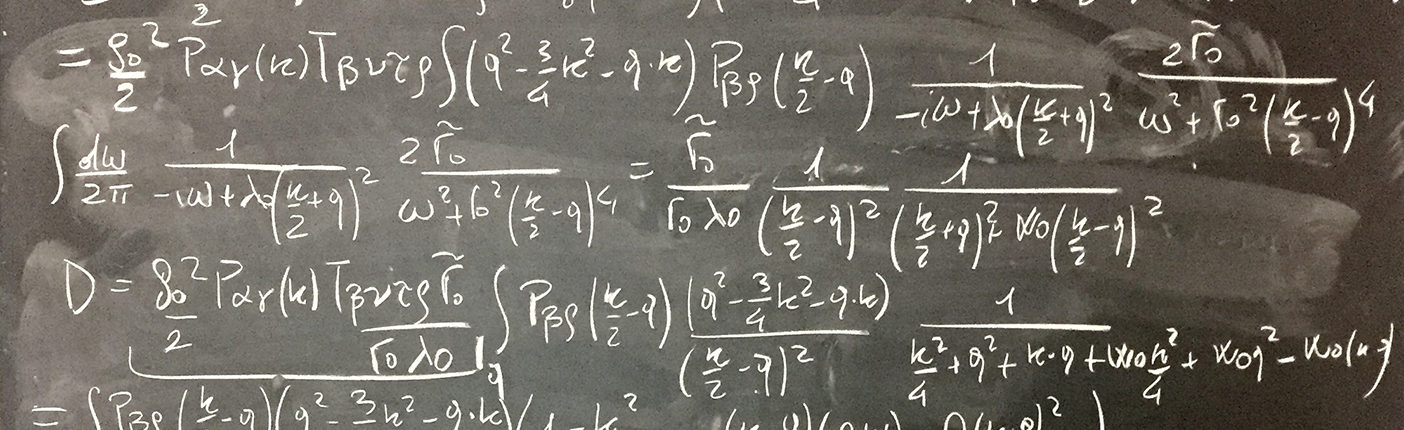
In the past decade the work of CoBBS lab showed that cornerstones of a physical description of biological systems displaying collective behaviour are the concepts of correlation and scaling. These systems are correlated to a degree which is unusually strong and which would require some fine tuning at the physical level. Strong correlations are at the same time the mystery of collective behaviour and the key to unlock this mystery. Indeed, they allow us to study and compare through the same theoretical looking glass systems as diverse as bird flocks, insect swarms and cell colonies: when correlations extend far beyond all microscopic length scales of the system, we have a strong basis to believe that details cannot matter a lot. This scenario suggests that the current landscape of scattered concepts (correlation, universality, scaling) can be brought to a theoretical closure through the main tool that physics developed half a century ago exactly to this aim, namely the Renormalization Group.
Scaling laws represent an empirical backup to test universality in different systems, indeed we discovered experimental evidences of those in both birds’ flocks and insect swarms. 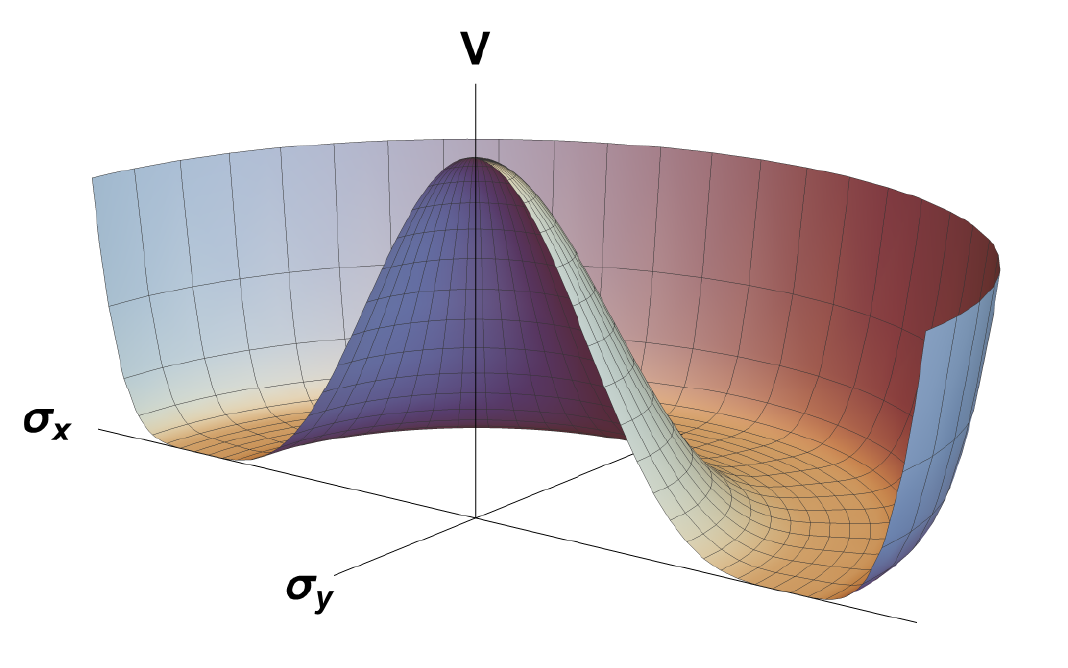 Therefore, we would like to define a theoretical approach able to give us the critical exponents both in ordered-flock phase and in the disordered-swarm phase, and to do this we need a new field theory. The novelty of the project lies both in the structure of the starting theory and in the RG technique that will be used. The renormalization procedure has to involve all the effects of out-of-equilibrium systems due to the self-propelled nature of the biological particles, while the new field theory has to reproduce important dynamic features as information transfer through the group. Unlike classical and dissipative models of active matter, the proposed theory is an inertial theory considering underlying symmetries of rotation and of information propagation already experimentally verified in flocks of birds and insect swarms.
Therefore, we would like to define a theoretical approach able to give us the critical exponents both in ordered-flock phase and in the disordered-swarm phase, and to do this we need a new field theory. The novelty of the project lies both in the structure of the starting theory and in the RG technique that will be used. The renormalization procedure has to involve all the effects of out-of-equilibrium systems due to the self-propelled nature of the biological particles, while the new field theory has to reproduce important dynamic features as information transfer through the group. Unlike classical and dissipative models of active matter, the proposed theory is an inertial theory considering underlying symmetries of rotation and of information propagation already experimentally verified in flocks of birds and insect swarms.
An additional ingredient has to be inserted in this description to consider not only phase fluctuations, but also speed fluctuations that in flocks are long-ranged correlated. To reproduce massless modes in the ordered phase of the model we introduce a novel confining potential for the full vector of the velocity (phase and speed). This potential has the interesting feature to produce divergent susceptibility and correlation length of the modulus of the degrees of freedom at null temperature. Therefore, in the deep ordered phase we can have a theoretical description of flocks’ scale-free correlations of speed.
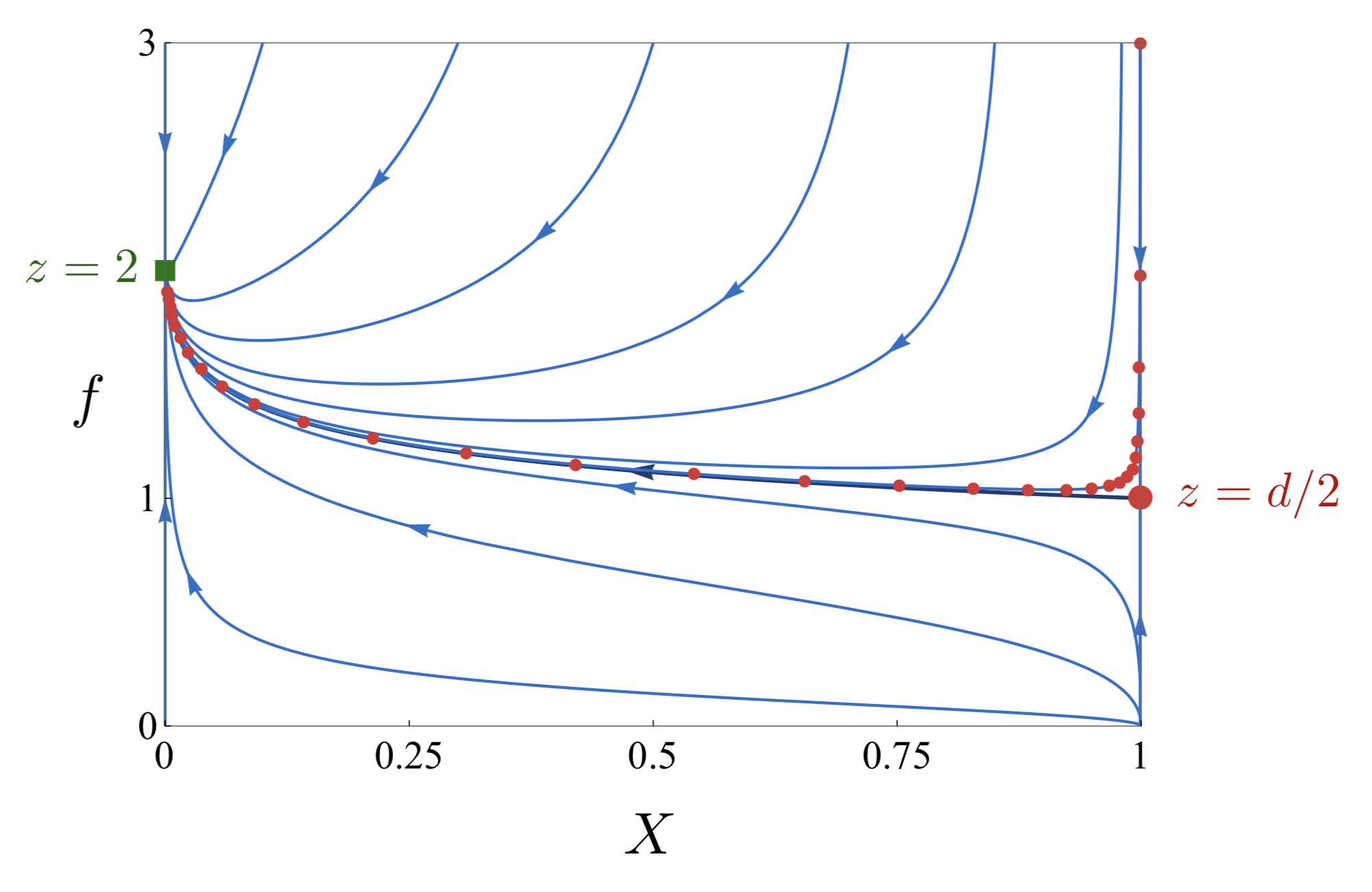 The inertial field theory that can reproduce key phenomena of collective behaviour is a rather intricate non-linear theory of three couple fields which has never been studied analytically before. A fixed network limit is then required to start an RG analysis of the theory. The new RG approach is going to combine standard Ɛ-expansion, where Ɛ is the deviation from the upper critical dimension, above which the linear theory holds, with new ingredients and methods to include the out-of-equilibrium nature of active systems. Studying these effects with renormalization is a hard task but it seems to be crucial to compute universal quantities as critical exponents that can represent an analytical explanation for the experimental results both of flocks and swarms.
The inertial field theory that can reproduce key phenomena of collective behaviour is a rather intricate non-linear theory of three couple fields which has never been studied analytically before. A fixed network limit is then required to start an RG analysis of the theory. The new RG approach is going to combine standard Ɛ-expansion, where Ɛ is the deviation from the upper critical dimension, above which the linear theory holds, with new ingredients and methods to include the out-of-equilibrium nature of active systems. Studying these effects with renormalization is a hard task but it seems to be crucial to compute universal quantities as critical exponents that can represent an analytical explanation for the experimental results both of flocks and swarms.
Essential elements to complete the global theoretical picture are relevant tools in statistical physics as a dynamical maximum entropy approach to infer directly from data the nature of the dynamical equations with the purpose of completely justifying the second order dynamics of the new theory; and extensive numerical simulations of microscopic active models. We strongly believe that numerical simulations are crucial to perform null case tests of each given tool of analysis of our empirical data and can be a useful guide in developing both new theory and new experiments.
