Nonlinear optics concerns all those phenomena depending on the intensity of light ranging from lasing process to extreme waves excitation like shock waves, solitons, and rogue waves. In our group, we are interested in studying the emergence of such phenomena in systems where the subtle interplay between structural complexity and nonlinearity has led to the observation of effects, whose analysis and comprehension has required the employment of dedicated theoretical techniques. In turn, the development of novel theoretical approaches has provided a deeper insight of known phenomena and has opened the road for very novel research fields.
DISPERSIVE SHOCK WAVES : FROM DISORDER TO IRREVERSIBILITY IN OPTICAL NONLOCAL MEDIA
Shock Waves in Disordered Media
N. Ghofraniha, S. Gentilini,V. Folli, E. DelRe,and C. Conti
Shock waves in disordered nonlocal media, Phys. Rev. Lett., 109(24), 243902 (2012).
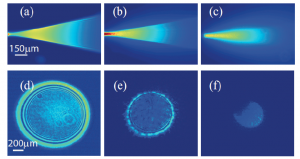
We experimentally investigate the interplay between spatial shock waves and the degree of disorder during nonlinear optical propagation in a thermal defocusing medium. We characterize the way the shock point is affected by the amount of disorder and scales with wave amplitude. Evidence for the existence of a phase diagram in terms of nonlinearity and amount of randomness is reported. The results are in quantitative agreement with a theoretical approach based on the hydrodynamic approximation.
Nonlinear Gamow vectors, shock waves, and irreversibility in optically nonlocal media
Silvia Gentilini, Maria Chiara Braidotti, Giulia Marcucci, Eugenio DelRe, and Claudio Conti
Nonlinear Gamow vectors, shock waves, and irreversibility in optically nonlocal media, Phys. Rev. A 92, 023801 (2015).
Dispersive shock waves in the absence of loss, these highly irregular and disordered waves are potentially reversible. However, no experimental evidence has been given about the possibility of inverting their dynamics and turn them into a regular wavefront. We introduce a theoretical formulation for the dynamics in a highly nonlocal and defocusing medium described by the nonlinear Schroedinger equation based on the concept of nonlinear Gamow vectors. We theoretically show that nonlinear Gamow vectors may be used as a generalized basis for describing the dynamics of the shock waves and affect the degree of irreversibility of wave-breaking phenomena. We also show that a nonlocal, nonlinear optical medium may act as a simulator for the experimental investigation of quantum irreversible models, as the reversed harmonic oscillator.
QUANTUM SOLITON
The study of nonlinear propagation of light at a quantum level may offer a complete a scenario to understand the action of nonlinearity at a low photon number regime can unveil unknown and totally new optical effects.
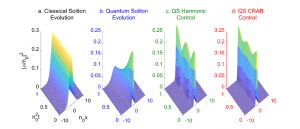
The first phenomenon we decided to investigate is the propagation of quantum optical solitons. In fact, though classical solitons (CSs) are very well studied, QSs have a much richer dynamics that may provide many new solutions for quantum computing and cryptography.
For this reason, we studied the fundamental properties of the soliton solution of the quantum nonlinear Schrödinger equation (QNLSE), first analytically and then numerically. We got the QNSE analytical solutions both by Bethe-ansatz and by quantum inverse scattering, whereas we obtained the numerical solutions by using phase-space methods, such as the Glauber- Sudarshan P-representation and the positive P-representation. This way we transformed operator equations in stochastic differential equations, solvable by a stochastic Runge-Kutta algorithm. The most important difference between the QSs and the CSs proved both by theory and by simulations, is given by the breaking of the shape-invariance during the propagation. Indeed, the numerical simulations show the quantum wave-packet spreading and the QS emission spectrum.
Controlling quantum nonlinear optical processes, as the generation of highly nonclassical states and broadband spectra, is a major challenge in optics. Specifically, controlling quantum solitons is a problem which is very broad in scope; one can control the number of generated solitons or their parameters as amplitude or speed. We focused our attention on the process of quantum spreading of solitons and on the increase of spectral emission, which can bring to supercontinuum generation. By combining stochastic partial differential equations and the so-called Chopped Random Basis Optimization (CRAB), we looked for the best control function to limit the quantum spreading. This result opens up a number of further possibilities for controlling quantum dynamics.