QUANTUM MACHINE LEARNING @ QuDIT:
methods traditionally developed for classical and quantum complex systems will be applied to optimize and characterize complex quantum computing machines and complex topological quantum states possibly establishing a relation between quantum computational complexity and quantum complex behavior.
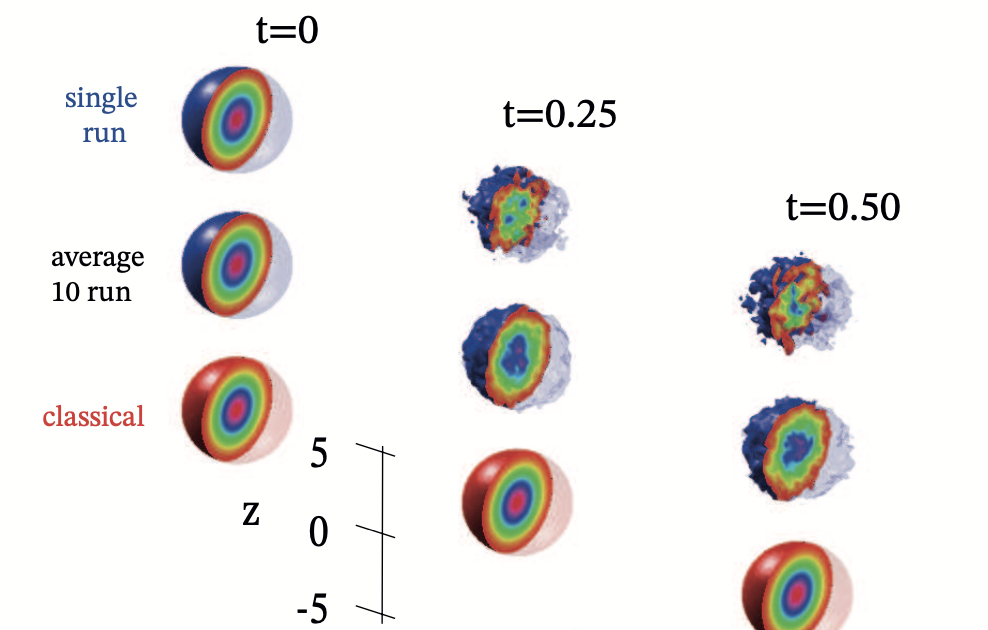
We use a neural network variational ansatz to compute Gaussian quantum discrete solitons in an array of waveguides described by the quantum discrete nonlinear Schroedinger equation. By training the quantum machine learning model in the phase space, we find different quantum soliton solutions varying the number of particles and interaction strength. The use of Gaussian states enables measuring the degree of entanglement and the boson sampling patterns. We compute the probability of generating different particle pairs when varying the soliton features and unveil that bound states of discrete solitons emit correlated pairs of photons. These results may have a role in boson sampling experiments with nonlinear systems and in developing quantum processors to generate entangled many-photon nonlinear states.
Claudio Conti, arxv:2110.12379 (2021)
Training Gaussian boson sampling by quantum machine learning
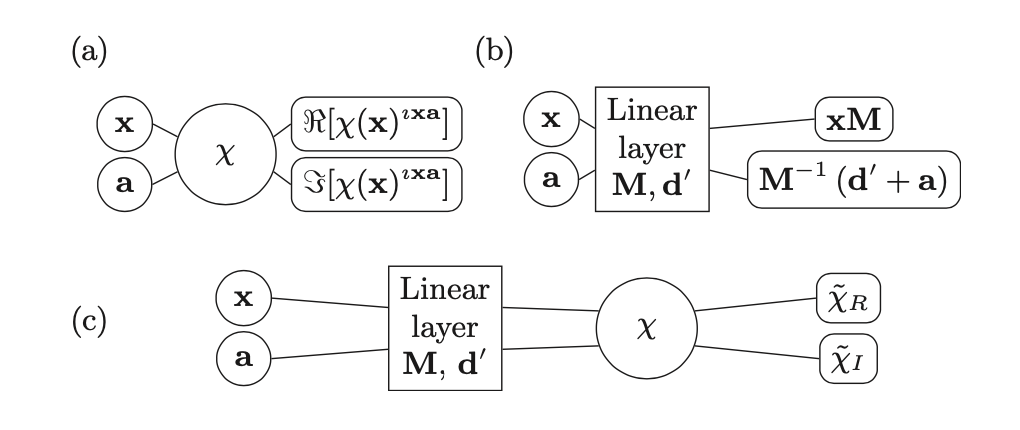
We use neural networks to represent the characteristic function of many-body Gaussian states in the quantum phase space. By a pullback mechanism, we model transformations due to unitary operators as linear layers that can be cascaded to simulate complex multi-particle processes. We use the layered neural networks for non-classical light propagation in random interferometers, and compute boson pattern probabilities by automatic differentiation. This is a viable strategy for training Gaussian boson sampling. We demonstrate that multi-particle events in Gaussian boson sampling can be optimized by a proper design and training of the neural network weights. The results are potentially useful to the creation of new sources and complex circuits for quantum technologies.
C. Conti, Quantum Machine Intelligence (2021) 3:26
WHAT QUANTUM OPTICS, QUANTUM INFORMATION AND QUANTUM MATERIAL THEORY CAN TEACH US ABOUT GRAVITY AND FUNDAMENTAL QUANTUM MECHANICS
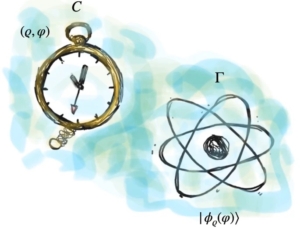
There is only one time
We draw a picture of physical systems that allows us to recognize what “time” is by requiring consistency with the way that time enters the fundamental laws of Physics. Elements of the picture are two non-interacting and yet entangled quantum systems, one of which acting as a clock. The setting is based on the Page and Wootters mechanism, with tools from large-N quantum approaches. Starting from an overall quantum description, we first take the classical limit of the clock only, and then of the clock and the evolving system altogether; we thus derive the Schrödinger equation in the first case, and the Hamilton equations of motion in the second. This work shows that there is not a “quantum time”, possibly opposed to a “classical” one; there is only one time, and it is a manifestation of entanglement.
C. Foti, A. Coppo, G. Barni and A Cuccoli, Nature Communications 12, 1787 (2021)
ULTRASTRONG LIGHT-MATTER COUPLING AND QUANTUM SENSING
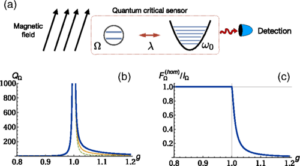
Critical Quantum Metrology with a Finite-Component Quantum Phase Transition
Physical systems close to a quantum phase transition exhibit a divergent susceptibility, suggesting that an arbitrarily high precision may be achieved by exploiting quantum critical systems as probes to estimate a physical parameter. However, such an improvement in sensitivity is counterbalanced by the closing of the energy gap, which implies a critical slowing down and an inevitable growth of the protocol duration. Here, we design different metrological protocols that exploit the superradiant phase transition of the quantum Rabi model, a finite-component system composed of a single two-level atom interacting with a single bosonic mode. We show that, in spite of the critical slowing down, critical quantum optical probes can achieve a quantum-enhanced time scaling of the sensitivity in frequency-estimation protocols.
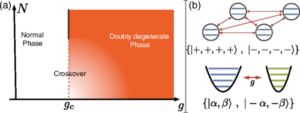
Universal Spectral Features of Ultrastrongly Coupled Systems
IWe identify universal properties of the low-energy subspace of a wide class of quantum optical models in the ultrastrong coupling limit, where the coupling strength dominates over all other energy scales in the system. We show that the symmetry of the light-matter interaction is at the origin of a twofold degeneracy in the spectrum. We prove analytically this result for bounded Hamiltonians and extend it to a class of models with unbounded operators. As a consequence, we show that the emergence of superradiant phases previously investigated in the context of critical phenomena, is a general property of the ultrastrong coupling limit. The set of models we consider encompasses different scenarios of possible interplay between critical behavior and superradiance.
QUANTUM DISSIPATIVE DYNAMICS IN THE BARDEEN-COOPER-SCHRIEFFER THEORY OF SUPERCONDUCTIVITY
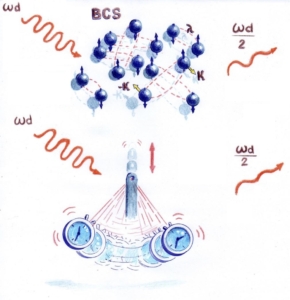
Emergent parametric resonances and time-crystal phases in driven Bardeen-Cooper-Schrieffer systems
We study the out-of-equilibrium dynamics of a Bardeen-Cooper-Schrieffer condensate subject to a periodic drive. We demonstrate that the combined effect of drive and interactions results in emerging parametric resonances, analogous to a vertically driving pendulum. In particular, Arnold tongues appear when the driving frequency matches 2Δ0/n, with n a natural number, and Δ0 the equilibrium gap parameter. Inside the Arnold tongues we find a commensurate time-crystal condensate which retains the U(1) symmetry breaking of the parent superfluid/superconducting phase and shows an additional time-translational symmetry breaking. Outside these tongues, the synchronized collective Higgs mode found in quench protocols is stabilized without the need of a strong perturbation. Our results are directly relevant to cold-atom and condensed-matter systems and do not require very long energy relaxation times to be observed.
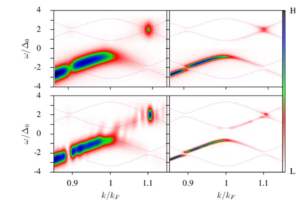
Nonlinear Dynamics of Driven Superconductors with Dissipation
In the absence of dissipation a periodically driven BCS superconductor can enter a coherent nonlinear regime of collective Rabi oscillations which last for arbitrary long times [Ojeda Collado et al., Phys. Rev. B 98, 214519 (2018)]. Here we show that dissipation effects introduce dramatic changes: (i) The collective Rabi mode becomes a transient. (ii) At long times a steady state is reached showing strong nonlinear effects for large enough drive strength. We identify the physical parameters governing the various crossovers and present a detailed computation of time- and angle-resolved photoemission spectroscopy (tr-ARPES) and time-resolved tunneling spectra aiming at detecting the collective Rabi oscillations and the steady-state nonlinearities. We show also that second harmonic generation is allowed for a drive which acts on the BCS coupling constant.
IconBox Title
Click to add your own text here
REal-time motion CorrEctioN in magneTic REsonance
REal-time motion CorrEctioN in magneTic REsonance
| Founding Body: | PRIN PNRR 2022. RESEARCH PROJECTS OF RELEVANT NATIONAL INTEREST – Call 2022 PNRR |
|---|---|
| Total grant: | € 299,735 (ISC € 18000) |
| Principal Investigators: | Stefano Giagu, Sapienza (PI) Silvia Capuani (co PI) CNR-ISC |
| Other participants: | Marco Montuori |
| Project duration: | 2023-2026 |
| Website: |
Newsletter ISC Febbraio-Marzo 2026
La nostra Newsletter di Febbraio-Marzo 2026 è disponibile!
Potete scaricare il pdf da qui: Newsletter feb mar 2026
Buona lettura!
REal-time motion CorrEctioN in magneTic REsonance
REal-time motion CorrEctioN in magneTic REsonance
| Founding Body: | PRIN PNRR 2022. RESEARCH PROJECTS OF RELEVANT NATIONAL INTEREST – Call 2022 PNRR |
|---|---|
| Total grant: | € 299,735 (ISC € 18000) |
| Principal Investigators: | Stefano Giagu, Sapienza (PI) Silvia Capuani (co PI) CNR-ISC |
| Other participants: | Marco Montuori |
| Project duration: | 2023-2026 |
| Website: |
Newsletter ISC Febbraio-Marzo 2026
La nostra Newsletter di Febbraio-Marzo 2026 è disponibile!
Potete scaricare il pdf da qui: Newsletter feb mar 2026
Buona lettura!
REal-time motion CorrEctioN in magneTic REsonance
REal-time motion CorrEctioN in magneTic REsonance
| Founding Body: | PRIN PNRR 2022. RESEARCH PROJECTS OF RELEVANT NATIONAL INTEREST – Call 2022 PNRR |
|---|---|
| Total grant: | € 299,735 (ISC € 18000) |
| Principal Investigators: | Stefano Giagu, Sapienza (PI) Silvia Capuani (co PI) CNR-ISC |
| Other participants: | Marco Montuori |
| Project duration: | 2023-2026 |
| Website: |
Newsletter ISC Febbraio-Marzo 2026
La nostra Newsletter di Febbraio-Marzo 2026 è disponibile!
Potete scaricare il pdf da qui: Newsletter feb mar 2026
Buona lettura!
REal-time motion CorrEctioN in magneTic REsonance
REal-time motion CorrEctioN in magneTic REsonance
| Founding Body: | PRIN PNRR 2022. RESEARCH PROJECTS OF RELEVANT NATIONAL INTEREST – Call 2022 PNRR |
|---|---|
| Total grant: | € 299,735 (ISC € 18000) |
| Principal Investigators: | Stefano Giagu, Sapienza (PI) Silvia Capuani (co PI) CNR-ISC |
| Other participants: | Marco Montuori |
| Project duration: | 2023-2026 |
| Website: |
Newsletter ISC Febbraio-Marzo 2026
La nostra Newsletter di Febbraio-Marzo 2026 è disponibile!
Potete scaricare il pdf da qui: Newsletter feb mar 2026
Buona lettura!
Force-free molecular dynamics on Nature Machine Intelligence
Lateral Stress on the Interfacial Water of Biological Membranes on ACS Materials and Interfaces
Il CNR per la semplificazione organizzativa e l’innovazione digitale