TOPOLOGY AS A TOOL FOR FUTURE DISCOVERIES
Topology provides a way to classify physical systems considering how their parts connect rather than just through usual properties like color, mass, length and microscopic symmetries.
Möbius strip is just a simple example of how topology is related to connection of different parts and of how strongly topology can change physical properties.
In condensed matter a number of effects can be directly related to the topological properties of the spectrum of a solid. Examples are the whole range of quantum Hall effects, Thouless pumping, the bulk-boundary coorespondence in topological insulators, topological supercondutivity. What makes these effects so interesting is their robustness, universality and independence on dynamical details; thanks to these unique features, topological effects are currently employed for metrological standards, topological states were proposed to robustly encode qubits and topological systems are often indicated as condensed matter analogues of quantum field theory models.
Our research in topological photonics aims at studying all these aspects in topological photonic materials.
TOPOLOGICAL PHOTONICS STORIES
Machine learning inverse problem for topological photonics
Laura Pilozzi, Francis Farrelly, Giulia Marcucci and Claudio Conti
Communications Physics, 1 57 (2018)
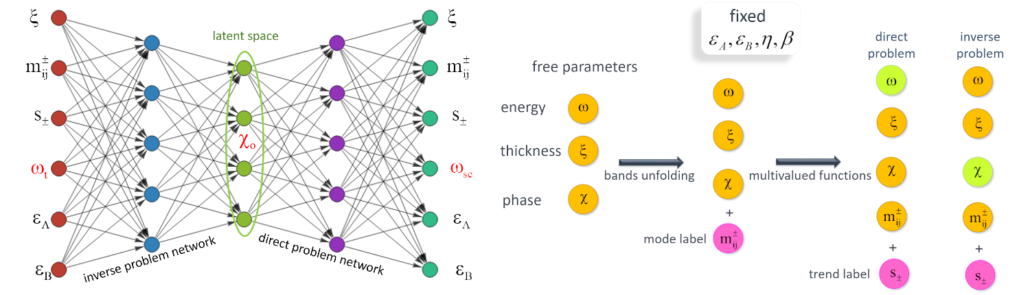
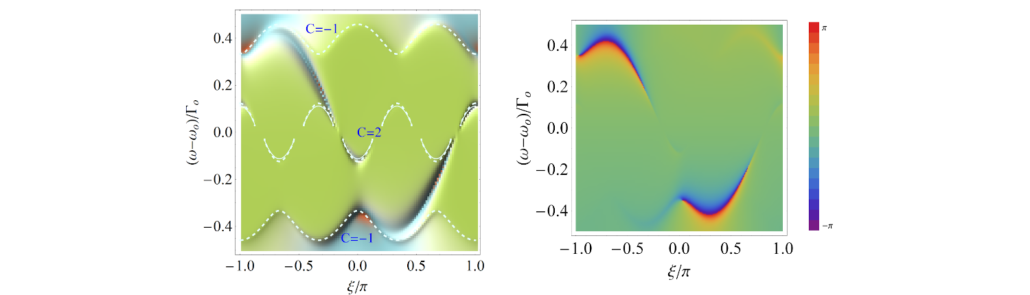
Topology opens many new horizons for photonics, from integrated optics to lasers. The complexity of large-scale devices asks for an effective solution of the inverse problem: how best to engineer the topology for a specific application? We introduce a machine-learning approach applicable in general to numerous topological problems. As a toy model, we train a neural network with the Aubry–Andre–Harper band structure model and then adopt the network for solving the inverse problem. Our application is able to identify the parameters of a complex topological insulator in order to obtain protected edge states at target frequencies. One challenging aspect is handling the multivalued branches of the direct problem and discarding unphysical solutions. We overcome this problem by adopting a self-consistent method to only select physically relevant solutions. We demonstrate our technique in a realistic design and by resorting to the widely available open-source TensorFlow library.
Topological lasing in resonant photonic structures
Laura Pilozzi and Claudio Conti
Phys. Rev. B 93, 195317 (2016)
We exploit topological edge states in resonant photonic crystals to attain strongly localized resonances and demonstrate lasing in these modes upon optical excitation. The use of virtually lossless topologically isolated edge states may lead to a class of thresholdless lasers operating without inversion. One needs, however, to understand whether topological states may be coupled to external radiation and act as active cavities. We study a two-level topological insulator and show that self-induced transparency pulses can directly excite edge states. We simulate laser emission by a suitably designed topological cavity and show that it can emit tunable radiation. For a configuration of sites following the off-diagonal Aubry-André-Harper model, we solve the Maxwell-Bloch equations in the time domain and provide a first-principles confirmation of topological lasers. Our results open the road to a class of light emitters with topological protection for applications ranging from low-cost energetically effective integrated laser sources, also including silicon photonics, to strong-coupling devices for studying ultrafast quantum processes with engineered vacuum.