Le neuroscienze: Dal cervello al neurone
Le neuroscienze, che si occupano di studiare il cervello ed il sistema nervoso, erano un tempo dominio di biologi, biochimici e fisiologici, ma sono ormai divenute un campo di ricerca assolutamente interdisciplinare che vede impegnati scienziati provenienti anche dalla matematica, la fisica, l’informatica e la scienza dei computer. Il trasferimento di metodologie proprie di queste discipline alle neuroscienze ha consentito di sviluppare modelli matematici e tecniche di analisi dati in grado di studiare il comportamento di sistemi complessi come il cervello.
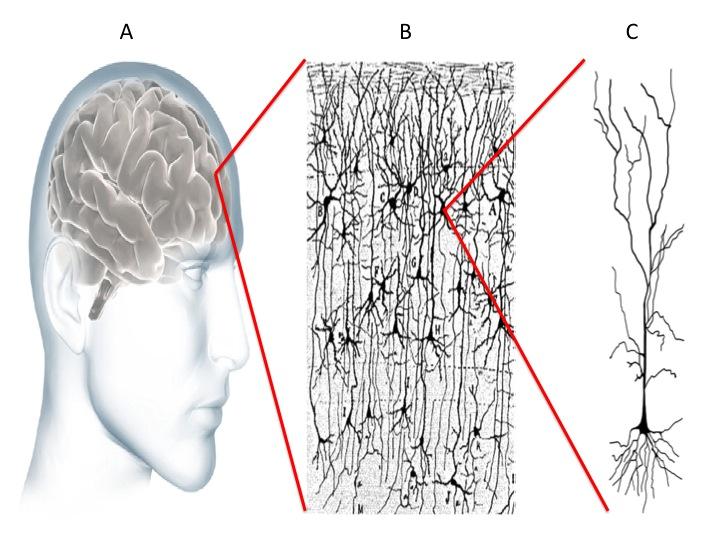
Fig. 1: A. Cervello umano. B. Rete neuronale. C. Neurone.
La principale sfida delle neuroscienze è rappresentata dallo studio dei meccanismi che sono alla base delle funzioni superiori svolte dal cervello umano. Il cervello (Figura 1A) è costituito da un insieme di reti neuronali (Figura 1B) ed ogni rete a sua volta è composta da un numero elevatissimo di neuroni (Figura 1C). In totale si arriva ad un numero astronomico di circa 100 miliardi di neuroni nell’intero cervello. La corteccia cerebrale, con uno spessore di circa 2-4mm ed una densità di circa 100.000 neuroni per millimetro cubo, rappresenta lo strato più esterno del cervello ed in essa sono individuabili aree deputate a svolgere principalmente alcune funzioni, come la percezione, il pensiero, la memoria e il linguaggio.
I neuroni e le sinapsi
I neuroni sono cellule specializzate del sistema nervoso che sono deputate al trasferimento, immagazzinamento e processamento delle informazioni. I neuroni scambiano tra loro informazioni attraverso l’emissione e la ricezione di segnali elettrici che sono generati da correnti che attraversano la membrana cellulare. Dal punto di vista della fisica i neuroni sono quindi essenzialmente dei dispositivi elettrici. Tipicamente, pur nella varietà di tipi di cellule neuronali, possiamo riconoscere tre parti che sono morfologicamente e funzionalmente distinte (Figura 2A): il corpo cellulare (o soma), i dendriti e gli assoni. Il soma ha una struttura compatta approssimativamente sferica ed è l’unità deputata all’elaborazione delle informazioni. I dendriti sono estensioni del soma con una struttura ramificata ed hanno la funzione di raccogliere i segnali elettrici provenienti dagli altri neuroni e trasmetterli al soma. Gli assoni, infine, sono lunghe protuberanze che si proiettano dal soma e che si occupano di trasmettere il segnale generato nel soma ai dendriti di un altro neurone.
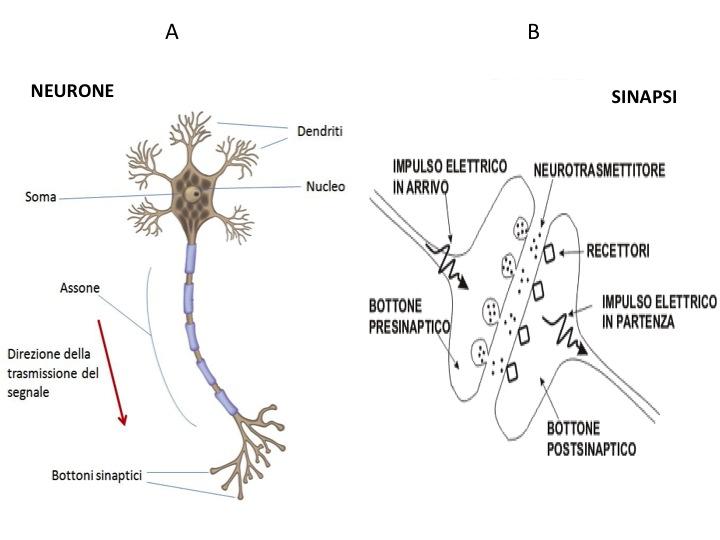
Fig. 2: A. Neurone (con soma, assone e dendriti). B. Sinapsi chimica.
La struttura attraverso la quale si realizza il trasferimento dell’impulso elettrico generato dal neurone pre-sinaptico (a monte) al neurone post-sinaptico (a valle) si chiama sinapsi (Figura 2B). Si distinguono essenzialmente due tipi di sinapsi: la sinapsi elettrica e la sinapsi chimica, quest’ultima risulta la più comune nel cervello dei vertebrati. La sinapsi elettrica realizza una giunzione elettrica diretta tra due neuroni. Nella sinapsi chimica invece il neurone presinaptico e postsinaptico non sono in contatto diretto ma sono fisicamente separati dalla fessura sinaptica e la trasmissione del segnale elettrico è mediata da particolari sostanze chimiche chiamate neurotrasmettitori. Si ha infatti prima sull’assone della cellula presinaptica la trasformazione dell’ impulso elettrico in un segnale chimico, quindi la diffusione del neurotrasmettitore attraverso la fessura sinaptica ed infine la successiva riconversione sul dendrite del neurone postsinaptico del segnale chimico in un segnale elettrico.
Potenziale di membrana
Quando si parla di segnale elettrico neuronale ci si riferisce specificatamente ad una grandezza fisica chiamata potenziale di membrana (Figura 3A) che rappresenta la differenza di potenziale misurabile ai capi di due elettrodi, uno posto all’interno della cellula e l’altro posto nel liquido extracellulare circostante. Quando il neurone non riceve stimolazioni elettriche dagli altri neuroni il potenziale di membrana assume un valore caratteristico denominato potenziale di riposo, tipicamente dell’ordine di -65mV, ovvero l’interno della cellula neuronale si trova ad un potenziale inferiore rispetto all’esterno. Quando invece il neurone riceve una quantità opportuna di stimolazioni elettriche allora esso può a sua volta emettere un impulso elettrico, noto come potenziale di azione, che viene trasferito attraverso i propri assoni ai dendriti di altre cellule neuronali.
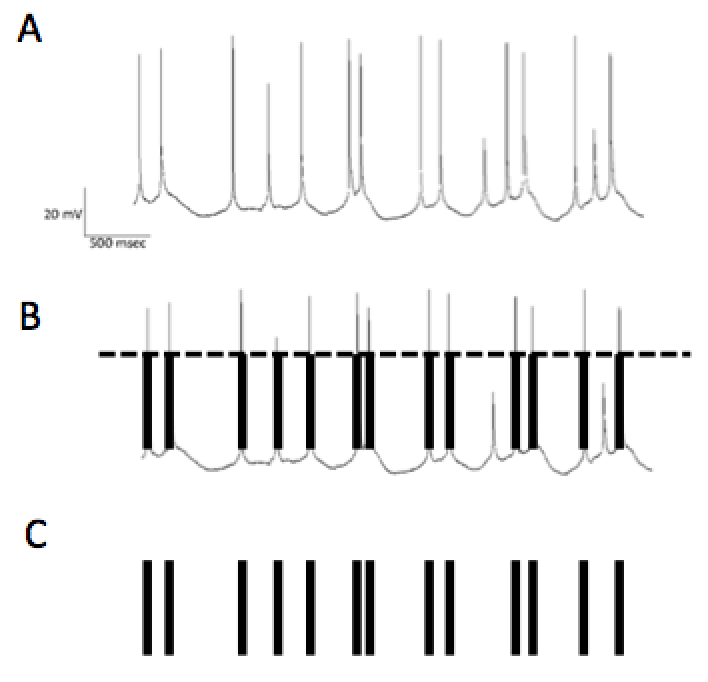
Fig. 3: A. Potenziale di membrana. B. Identificazione dei potenziali di azione. C. Treno di impulsi.
Il potenziale di azione ha una forma stereotipata e costituisce l’unità elementare di informazione associata alla trasmissione dei segnali neuronali. I potenziali di azione sono individuati quando il potenziale di membrana supera una determinata soglia (Figura 3B). Tipicamente quando ci si riferisce al segnale elettrico emesso da un neurone si intende la sequenza temporale di questi potenziali di azione, detta anche treno di impulsi (Figura 3C).
Reti di neuroni
I neuroni (Figura 4A) risultano connessi tra loro in modo anche molto intricato in strutture chiamate reti (Figura 4B). Il concetto di rete è molto generale e si applica agli ambiti più disparati. Si pensi ad esempio alle reti di trasmissione dell’energia elettrica, alle reti sociali, ad internet che realizza una rete di computer. In ogni caso una rete si caratterizza per la presenza di nodi e connessioni tra i nodi. Le reti possono essere organizzate in topologie molto complesse e possono essere costituite a loro volta da sottoreti. Nel caso delle reti neurali i nodi sono ovviamente rappresentati dai neuroni e le connessioni sono le sinapsi.
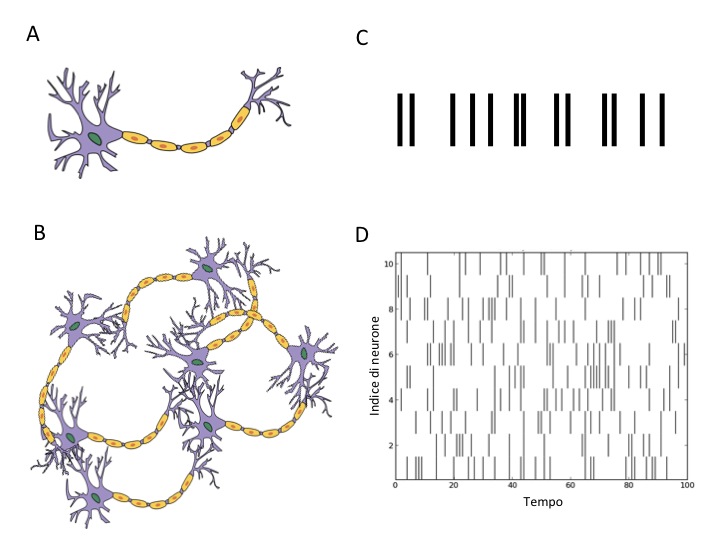
Figura 4: A. Singolo neurone. B. Rete neuronale. C. Treno di impulsi di un singolo neurone. D. Attività della rete neuronale (raster plot).
Il segnale di un neurone può essere ridotto alla sola successione dei tempi a cui sono emessi i potenziali di azione (Figura 4C). Per descrivere graficamente l’attività di una rete si ricorre in genere ad un tipo di grafico (chiamato con un termine inglese raster plot) dove ogni punto rappresenta l’emissione di un potenziale di azione ad un certo istante di tempo da parte di un determinato neurone (Figura 4D).
Modelli matematici neuronali
Negli anni cinquanta del ‘900 esperimenti pionieristici condotti da Hodgkin e Huxley (Figura 5) sulla fisiologia del neurone hanno consentito ai due scienziati di sviluppare un modello matematico in grado di riprodurre quantitativamente il segnale elettrico prodotto da una particolare fibra nervosa, l’assone gigante del calamaro. Il modello di Hodgkin-Huxley è stato il primo a descrivere la dinamica neuronale ed ha portato i due autori del modello ad essere insigniti del premio Nobel per la medicina nel 1963. Da allora sono stati sviluppati modelli per altri tipi di neuroni i quali comunque si basano sul paradigma costituito dal modello di Hodgkin-Huxley.

Figura 5: Alan L. Hodgkin e Andrew F. Huxley
Come nasce in effetti il modello matematico del neurone? La membrana cellulare del neurone è costituita da un doppio strato lipidico ed è attraversata da veri e propri canali (canali ionici) i quali mettono in comunicazione l’interno e l’esterno della cellula, dove si trovano disciolte in una soluzione acquosa varie specie ioniche. La membrana cellulare ha proprietà elettriche misurabili e la schematizzazione più semplice è considerare il neurone come un circuito elettrico dove è presente: (i) una capacità elettrica (che tiene conto delle proprietà isolanti del doppio strato lipidico), (ii) un conduttore di elettricità (per la presenza dei canali ionici), ed anche (iii) una batteria con una tensione pari al potenziale di riposo.
Dalla modellizzazione del singolo neurone si arriva a costruire il modello di una intera rete neuronale aggiungendo anche la modellizzazione delle sinapsi. Alla fine, il modello di un singolo neurone o di una rete è descritto da un insieme di equazioni matematiche le cui soluzioni rappresentano i comportamenti del sistema.
Analisi dati neuronali
Durante gli ultimi anni sono state sviluppate tantissime tecniche per analizzare dati neuronali. Uno degli strumenti di analisi più importanti è la misura del livello di sincronizzazione tra treni di impulsi. Questa tecnica permette distinguere diversi comportamenti di una rete come la sincronizzazione (Figura 6A), quando tutti i neuroni emettono i loro impulsi contemporaneamente, o viceversa la antisincronizzazione (Figura 6B), quando i neuroni della rete emettono i loro impulsi in sequenza come una catena.
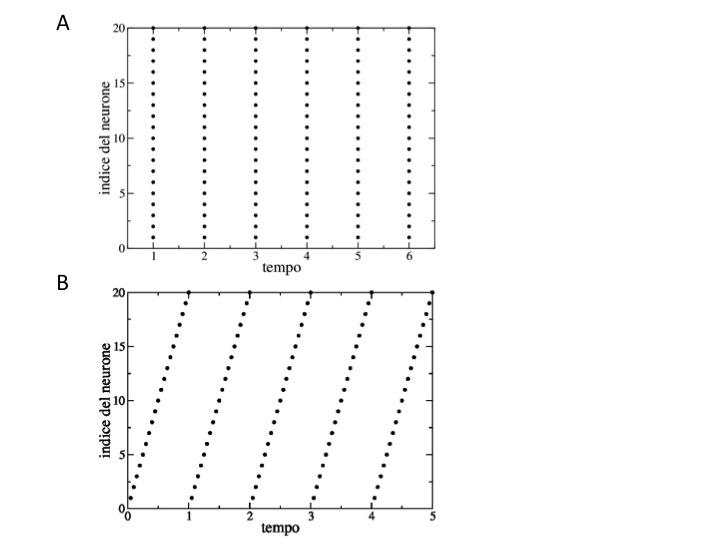
Figura 6: Esempi di comportamento di una rete di 20 neuroni. A. Sincronizzazione B. Antisincronizzazione.
Ci sono tante applicazioni importanti per questo tipo di analisi. Può essere usata per quantificare la fedeltà della risposta di un neurone a cui viene sottoposto ripetutamente un medesimo stimolo ovvero per quantificare il trasferimento di informazione tra neuroni accoppiati in una rete. Infine, la sincronizzazione tra neuroni è di cruciale importanza anche per malattie del sistema nervoso come il Parkinson o l’epilessia. Per esempio, un attacco epilettico è caratterizzato da un livello molto elevato di sincronizzazione neuronale.
Approfondimenti
Ulteriori informazioni sulle due direzioni di ricerca effettuate nel nostro istituto possono essere trovate in queste pagine web:
1. Modellizzazione reti Computational Neuroscience Lab Florence (in inglese)
2. Analisi dati neuronali Institute homepage Thomas Kreuz (in inglese)
